ROC czyli Receiver Operating Characteristic to temat, który zaskoczył mnie, kiedy podczas pracy nad jednym z moich projektów czytałam na temat przeprowadzanych badań medycznych. Pojawił się wraz z pojęciem AUC. I tak jak mi się wydawało, że o macierzy błędów wiem już wszystko, tak nagle się okazało, że wcale tak nie jest i dużo muszę jeszcze się nauczyć. Zapraszam do wspólnej nauki razem ze mną.
Zgodnie z definicją: ROC to graficzne narzędzie, które jest wykorzystywane do oceniania zdolności klasyfikatora binarnego do rozróżniania między dwoma klasami. Definicja definicją, ale czym są te klasyfikatory binarne? I dlaczego warto je porównywać?
Binarne klasyfikatory, to takie, w których klasyfikujemy nasze obserwowane obiekty do dwóch różnych grup. Na przykład spam i nie-spam albo nasze jabłka i pomidory z przykładu o macierzy błędów. A dlaczego warto porównywać – to właśnie zaraz wytłumaczę na przykładach.
Małe przypomnienie
Być może pamiętacie, że pisałam Wam w tekście o klasyfikacji tekstu, że można skorzystać z różnych algorytmów. Na przykład można użyć drzew decyzyjnych, regresji logistycznej albo wykorzystać bardziej nowoczesne sieci neuronowe. I każda z tych metod w jakiś tam sposób pozwoli na odpowiednie sklasyfikowanie tekstu. I najprawdopodobniej w każdej z tych metod będą jakieś błędy. Być może któryś klasyfikator będzie miał tendencję więcej przykładów wrzucać do kategorii A, a mniej do B. Być może jakieś konkretne przykłady będzie wrzucał do kategorii A. Pierwszy może mylić się częściej a drugi rzadziej. Klasyfikatorów jest dużo, a my chcemy wybrać jeden z nich i wybrać go tak, żeby jak najlepiej spełniał nasze oczekiwania.
Dosyć teorii! Póki sama próbowałam czytać tylko teoretycznie, o co w tym chodzi, to mnie nie przekonywało. A jak zabrałam się za rysowanie, to jakoś wszystko w głowie się poukładało. Więc proponuję, żebyśmy porysowali razem. Wróćmy do przykładu jabłek i pomidorów z tekstu o macierzy błędów. Pamiętacie?
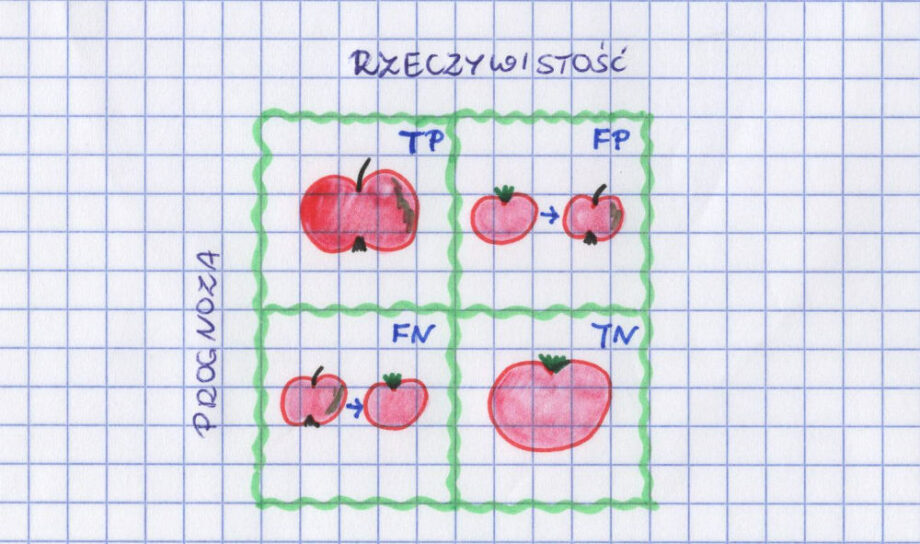
Mamy jabłka i pomidory. Naszą klasą „pozytywną” są jabłka, a „negatywną” pomidory. Jeśli prawidłowo je zaklasyfikujemy, to mamy do czynienia z TP i TN (True Positive i True Negative). Jeżeli pomylimy pomidora i powiemy, że jest jabłkiem, to mamy FP – False Positive (coś nieprawidłowo zostało zaklasyfikowane do zbioru pozytywów, mimo że nim nie jest). Jeśli jabłko zostanie uznane za pomidora, to mamy FN – False Negative.
Oprócz tego musimy przypomnieć sobie, czym jest TPR i FPR, bo to one znajdują się na wykresie:
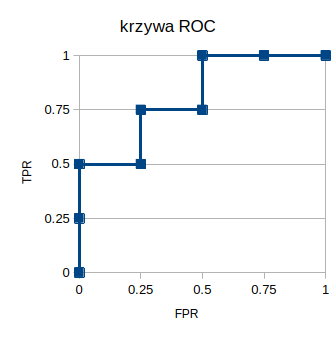
\(TPR=\frac{TP}{P}=\frac{TP}{TP+FN}\) \(FPR=\frac{FP}{N}=\frac{FP}{FP+TN}\)Krzywa ROC – przykład jabłka i pomidory – klasyfikator 1
Dobra. Tyle tytułem przypomnienia. Teraz konkretny przykład. Mamy 4 jabłka i 4 pomidory. Każemy klasyfikatorowi numer 1 posortować je tak, żeby najpierw były jabłka, a potem pomidory. Załóżmy, że zrobi to następująco: jabłko, jabłko, pomidor, jabłko, pomidor, jabłko, pomidor, pomidor. Zerknijmy teraz od lewej strony. Mamy w tej samej kolejności narysowane nasze jabłka i pomidory, a do tego dorzucamy macierz błędów gdybyśmy chcieli w danym miejscu postawić granicę między jabłkami a pomidorami.

W pierwszym momencie uznajemy, że wszystko jest pomidorem. Po lewej stronie od macierzy błędów jest zero jabłek i zero pomidorów. Po prawej są 4 jabłka (FN) i 4 pomidory (TN). Obliczamy TPR i FPR. Obydwa wynoszą 0. Przesuwamy naszą linię odcięcia pomiędzy jabłkami i pomidorami o jeden obiekt w prawo. Teraz jedno jabłko uznajemy za jabłko, a wszystko co jest po prawej za pomidory. W naszej macierzy błędów na tym etapie mamy jedno prawidłowo przypisane jabłko (TP), 3 błędnie zaklasyfikowane jabłka (FN), 0 błędnie zaklasyfikowanych pomidorów (FP) i 4 prawidłowo zaklasyfikowane pomidory (TN). TPR wynosi już 1/4, FPR to nadal 0, bo nie mamy żadnego błędnie zaklasyfikowanego pomidora. Potem mamy 2 prawidłowo zaklasyfikowane jabłka i odpowiednio TPR i FPR 1/2 oraz 0. W następnym kroku dochodzimy do pierwszego pomidora. Zostaje on zaklasyfikowany jako jabłko i pojawia się pierwsze FP w efekcie mamy TPR i FPR 1/2 i 1/4. Kontynuujemy naszą analizę aż do momentu, kiedy wszystko klasyfikujemy jako jabłka i dochodzimy do etapu, że TPR wynosi 1 i tyle samo wynosi FPR. Następnie wszystko przedstawiamy na wykresie i powstaje nam krzywa ROC:
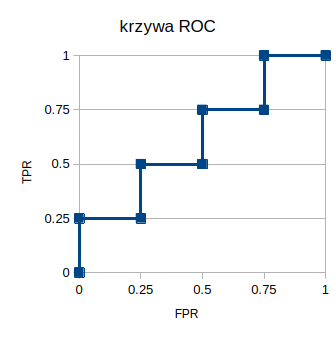
Krzywa ROC – przykład jabłka i pomidory – klasyfikator 2
Weźmy teraz klasyfikator numer 2. Również miał posortować nasze obiekty według prawdopodobieństwa bycia jabłkiem. No to ustawił te nasze „jabłka” od lewej strony następująco: jabłko, pomidor, jabłko, pomidor, jabłko, pomidor, jabłko, pomidor. Jak widać pomieszanie z poplątaniem. Ale tutaj jeszcze chcę wyjaśnić jedną rzecz. Bo na moim obrazku wszystkie jabłka wyglądają identycznie i wszystkie pomidory wyglądają identycznie. W rzeczywistości tak nie jest. Każdy owoc i każde warzywo różnią się między sobą. Dlatego różnie mogą działać klasyfikatory. Jeden większą wagę przyłoży do wielkości obiektu. Inny do koloru. Trzeci być może skupi się na „ogonku”. To dlatego pomidory mogą mieć większe prawdopodobieństwo bycia jabłkiem niż jabłka same w sobie.
Jak już wyjaśniłam, skąd może się brać kolejność, to przejdźmy do macierzy błędów, obliczeń TPR i FPR i krzywej ROC. Działamy tak samo jak w pierwszym przykładzie. Jeśli chcecie jak najlepiej to zrozumieć, to spróbujcie samodzielnie wpisać wszystkie wartości do macierzy błędów i następnie obliczcie sobie TPR i FPR. Możecie też samodzielnie narysować krzywą ROC.

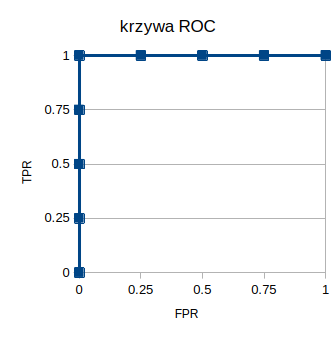
Krzywa ROC – przykład jabłka i pomidory – klasyfikator 3
A teraz piękny idealny klasyfikator. Posegregował nam najpierw jabłuszka, a potem pomidory. Czyli dokładnie tak, jak byśmy chcieli. I krzywa ROC w takiej sytuacji układa się w bardzo charakterystyczny sposób. Najpierw przy zerowym FPR, TPR rośnie krok po kroku do jedynki, a następnie FPR też rośnie do jedynki.

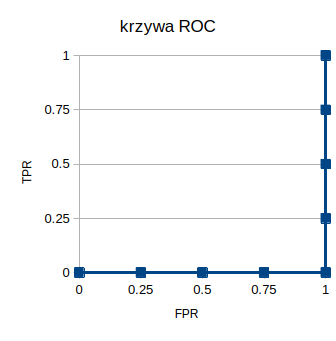
Krzywa ROC – przykład jabłka i pomidory – klasyfikator 4
No i całkowite przeciwieństwo idealnego klasyfikatora. Najpierw rolę jabłek przypisuje wszystkim pomidorom, a dopiero później segreguje jabłka. Krzywa ROC „szoruje po dnie”, czyli dla zerowego TPR rośnie krok po kroku FPR, a dopiero kiedy FPR wynosi 1, to zaczyna rosnąć również TPR.
Wydawałoby się, że taki klasyfikator do niczego się nie nadaje, ale czy oby na pewno? Tak naprawdę jest on tak samo dobry jak ten poprzedni. Wystarczy tylko mu powiedzieć, że wynik jest przeciwny do uzyskanego i znów mamy idealne rozwiązanie.

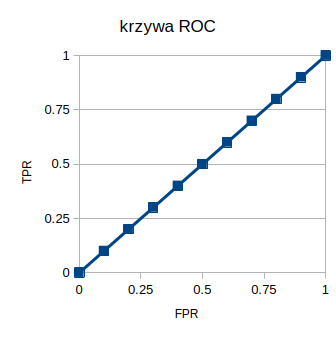
krzywa ROC – losowy klasyfikator
No właśnie. Jaka krzywa ROC jest dobra, a jaka niedobra? Tak naprawdę dla losowego klasyfikatora krzywa ROC wygląda następująco:
I można powiedzieć, że dla większości przypadków to będzie najgorszy klasyfikator. Dlaczego? Bo wszystko co jest na lewo od tej krzywej klasyfikuje lepiej. A wszystko co jest na prawo od tej krzywej można „zamienić miejscami” i już będzie po lewej.
Dlaczego mogą interesować nas różne klasyfikatory, a nawet różne progi odcięcia tych samych klasyfikatorów?
Dlaczego odpowiedni wybór klasyfikatorów i ich parametrów może być tak ważny? Dopóki poruszamy się w świecie jabłek i pomidorów, to nie ma to aż tak dużego znaczenia. Natomiast możemy sobie wyobrazić takie sytuacje, kiedy jest to szczególnie ważne. Weźmy pod uwagę medycynę i testy sprawdzające czy ktoś jest chory czy zdrowy. Jeśli kogoś, kto nie jest chory, błędnie zaklasyfikujemy do grupy zarażonych, to konsekwencją będzie fakt, że zostanie poddany dokładnej obserwacji i starannie przebadany. Jeśli natomiast osobie chorej powiemy, że jest zdrowa i nie wdrożymy odpowiedniego leczenia, to skutki mogą być tragiczne. Tak więc w tym przypadku „False Positive” (błędnie uznane za chorego) jest dużo mniej groźne od „False Negative” (czyli chory przekonany o swoim zdrowiu). I spośród wszystkich klasyfikatorów i możliwych progów odcięcia chcemy wybrać taki, który pozwoli nam z jak najmniejszą szkodą dla osób zdrowych, wyłapywać jak najwięcej przypadków osób zarażonych.
ROC – ciekawostki
Pora też na małą ciekawostkę. Krzywa ROC powstała podczas drugiej wojny światowej. Była używana w dziedzinie radarów do analizy wydajności odbiorników w detekcji obiektów. Dopiero dużo później została dostosowana do problemów klasyfikacyjnych. Z pochodzenia krzywej ROC bierze się jej nazwa – w polskim tłumaczeniu: charakterystyka pracy odbiornika. Ale raczej nie spotyka się tej nazwy, najczęściej widywałam informacje na jej temat po prostu ze skrótem ROC i tyle.
I jeszcze informacja o jednej z zalet: krzywa ROC dostarcza informacji o zdolności modelu do rozróżniania między dwiema klasami, ale nie uwzględnia rozkładu klas w zbiorze danych. Dlatego może być przydatna przy problemach, gdzie klasy są nierównomiernie rozłożone. Właśnie dlatego krzywe ROC są często używane w medycynie, zwłaszcza w diagnostyce, aby ocenić zdolność testów diagnostycznych do poprawnego identyfikowania pacjentów z chorobą.
ROC – oczami ChatGPT
Zapytałam też ChatGPT, dlaczego wiedza na temat krzywej ROC jest istotna. Oto powody, którymi podzieliła się ze mną sztuczna inteligencja:
- Ocena skuteczności modeli klasyfikacyjnych: Krzywa ROC umożliwia obiektywną ocenę skuteczności klasyfikatorów binarnych w różnych dziedzinach, od medycyny po uczenie maszynowe.
- Porównywanie modeli: Pozwala na porównywanie wydajności różnych modeli klasyfikacyjnych, co jest niezbędne przy podejmowaniu decyzji dotyczących wyboru najlepszego modelu.
- Optymalizacja punktu odcięcia: Pomaga w optymalizacji punktu odcięcia w klasyfikatorach binarnych, co pozwala na dostosowanie klasyfikacji do konkretnych wymagań lub priorytetów.
- Rozumienie równowagi między czułością a specyficznością: Pomaga w zrozumieniu i ocenie równowagi między zdolnością do wykrywania pozytywnych przypadków a unikaniem fałszywie pozytywnych wyników.
- Uwzględnienie kosztów błędów klasyfikacji: Pozwala na uwzględnienie różnych kosztów błędów klasyfikacji, co jest istotne przy podejmowaniu decyzji biznesowych lub medycznych.
Wydaje mi się, że muszę się z nią (czyli z tą sztuczną inteligencją) zgodzić.
Artykuł ten powstał na blogu po długiej przerwie. Mam nadzieję, że wciąż jeszcze o mnie pamiętacie i że z przyjemnością przeczytaliście to co dla Was właśnie stworzyłam. Jeśli chcecie wrócić do starszych artykułów – zapraszam do skorzystania ze spisu treści. Jeżeli chcecie zajrzeć na stronę facebooka – również serdecznie zapraszam. Jeśli chcecie czymś się ze mną podzielić, to piszcie na adres mailowy [email protected].
Jeśli natomiast chcecie powiedzieć mi „Dzięki, Krysiu, zrobiłaś kolejny kawałek dobrej roboty”, to zawsze możecie mi kupić „kawkę”. Kawy nie pijam więc kawka będzie tylko przysłowiowa, ale gwarantuję, że będę za nią bardzo wdzięczna.
Dziękuję Wam wszystkim za to, że czytacie to, co dla Was tu piszę! Życzę miłego dnia!
Krystyna Piątkowska