Nie wiem dlaczego, ale jak myślę o rozproszeniu, to pierwsza rzecz, jaka przychodzi mi do głowy to Terry Pratchett i jego „Trzy wiedźmy”:
— Co teraz, sierżancie?
— My… rozproszymy się — odpowiedział. — Tak. Rozproszymy się. Tak właśnie zrobimy.
Ostrożnie sunęli przez paprocie. Sierżant przykucnął za poręcznym pniem.
— Dobrze — szepnął. — Bardzo dobrze. Złapaliście mniej więcej, o co zasadniczo chodzi. A teraz rozproszymy się znowu, ale tym razem rozproszymy się osobno.
Terry Pratchett „Trzy wiedźmy”
W czasie, kiedy sierżant szkoli swoich ludzi i tłumaczy, na czym polega rozproszenie w paprociach, ja spróbuję wytłumaczyć, o co chodzi z rozproszeniem w statystyce. Przypomnę Wam miary rozproszenia, które już opisywałam i opowiem o tych, których jeszcze nie przedstawiałam. Miłej lektury!
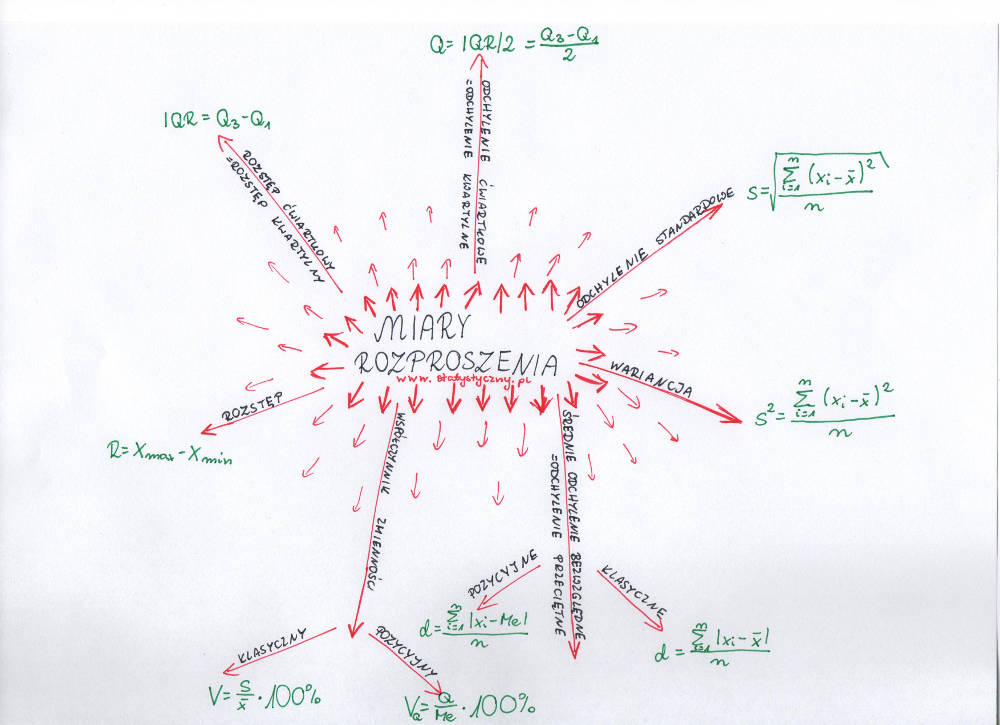
Odchylenie standardowe, o którym pisałam ostatnio, jest właśnie jedną z miar rozproszenia. Ale nie jedyną. Żeby to usystematyzować, postanowiłam zrobić wpis podsumowujący wszystkie miary rozproszenia, które już gdzieś przy okazji w różnych wpisach się pojawiły i uzupełnić o te, które jeszcze nie miały okazji się pojawić.
A co to w ogóle są miary rozproszenia? To takie miary rozkładu, które badają zróżnicowanie wartości cechy wokół wartości centralnych (najczęściej wokół średniej arytmetycznej, ale również można obliczyć miary rozproszenia dla mediany). Czyli łopatologicznie mówiąc mamy jakąś średnią i nasze badane obiekty albo mogą być do niej bardzo podobne (czyli mieć podobne wartości) albo zupełnie inne (i mieć wartości zupełnie niepodobne, rozproszone z dala od średniej). Miary rozproszenia badają, jak bardzo niepodobne do średniej są nasze badane jednostki statystyczne (jeśli są niepodobne, to obliczenie wartości centralnej niewiele nam powie o populacji, a jeśli są podobne, to oznacza, że średnia labo mediana dobrze reprezentują wszystkie jednostki). A oprócz nazwy miary rozproszenia możemy również używać sformułowania miary zmienności, miary zróżnicowania lub miary dyspersji. Wszystko znaczy to samo. Zamiast więc skupiać się na nazewnictwie, przejdźmy do analizy poszczególnych przykładów:
1. Odchylenie standardowe
mówi o tym, o ile średnio odchylają się wartości badanej cechy od średniej arytmetycznej. Jest najbardziej popularną i najczęściej stosowaną miarą rozproszenia. Wzór już był, ale na wszelki wypadek przypominam:
\(s=\sqrt{\frac{\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}}{n}}=\sqrt{\frac{(x_{1}-\overline{x})^{2}+(x_{2}-\overline{x})^{2}+\ldots+(x_{n}-\overline{x})^{2}}{n}}\)Przykłady wykorzystania odchylenia standardowego były opisane tydzień temu. Jeśli ktoś przegapił – warto przeczytać.
2. Wariancja
\(s^{2}=\frac{\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}}{n}=\frac{(x_{1}-\overline{x})^{2}+(x_{2}-\overline{x})^{2}+\ldots+(x_{n}-\overline{x})^{2}}{n}\)Czy ktoś zauważył, czym się różni wariancja od odchylenia standardowego? Tylko i wyłącznie brakiem pierwiastka. Tak naprawdę, żeby obliczyć odchylenie standardowe, to najpierw musimy wyliczyć właśnie wariancję. Dlaczego więc jest mniej popularna w statystycznej analizie opisowej? Przede wszystkim dlatego, że wartość wariancji jest wyrażona w kwadracie jednostki (czyli jak liczymy średni wzrost, to wariancję mamy w metrach kwadratowych, a jak liczymy średnie zużycie długopisów, to wynik jest w… długopisach kwadratowych). Dużo wygodniej jest wyciągnąć z tej wartości pierwiastek i operować wskaźnikiem, który ma taką samą jednostkę jak analizowana cecha.
3. Średnie odchylenie bezwzględne = odchylenie przeciętne
\(d=\frac{\sum_{i=1}^{n}|x_{i}-\overline{x}|}{n}\)Średnie odchylenie bezwględne występuje w dwóch wersjach – klasycznej i pozycyjnej. Można obliczać, o ile przeciętnie wszystkie wartości badanej cechy odchylają się od średniej artymetycznej (wzór powyżej, wersja klasyczna) albo o ile odchylają się od mediany (wzór poniżej, wersja pozycyjna).
\(d=\frac{\sum_{i=1}^{n}|x_{i}-Me|}{n}\)Odchylenie przeciętne jest bardzo podobne do odchylenia standardowego – tylko zamiast liczyć kwadraty i następnie je pierwiastkować, korzystamy z wartości bezwględnej, która również pomaga pozbyć się ujemnych odległości od średniej.
Uwaga! Gdybyśmy policzyli tylko odległości od średniej (bez wykorzystania wartości bezwzględnej), to sumarycznie otrzymalibyśmy wartość równą zero (co tylko potwierdza „średniowatość” średniej, która polega właśnie na tym, żeby sumarycznie wszystkie wartości były do niej jak najbardziej zbliżone).
4. Współczynnik zmienności
liczymy zarówno dla miar klasycznych jak i dla pozycyjnych.
W przypadku miar klasycznych (średnia arytmetyczna i odchylenie standardowe) współczynnik zmienności prezentuje się następująco:
\(V=\frac{s}{\overline{x}}*100\%\)W przypadku miar pozycyjnych (mediana i odchylenie ćwiartkowe) współczynnik zmienności liczymy za pomocą takiego wzoru:
\(V_{Q}=\frac{Q}{Me}*100\%\)Przypominam, że wyrażamy go w procentach. A co oznacza? Mówi o tym, jak bardzo rozproszona jest nasza populacja. Im wyższa wartość współczynnika zmienności, tym większe rozproszenie populacji (i tym gorzej średnia arytmetyczna reprezentuje populację, w związku z czym ma mniejszą wartość poznawczą).
Tutaj wypada się zastanowić, dlaczego porównując rozproszenie w dwóch różnych populacjach używa się współczynnika zmienności, a nie odchylenia standardowego. Załóżmy, że w dwóch piekarniach pieczemy ciasteczka. Jedna piecze małe ciasteczka o średniej wadze 10 gram, a druga większe ciastka o średniej wadze 50 gram. Jeśli odchylenie standardowe od średniej wagi w obu przypadkach wyniesie 3 gramy, to wcale nie oznacza, że zróżnicowanie wagi ciastek w obu piekarniach jest takie samo. W pierwszym przypadku mamy do czynienia z małymi ciasteczkami i różnica 3 gram jest proporcjonalnie dość spora (współczynnik zmienności wyniesie 30% i mówi o średnim zróżnicowaniu populacji). W przypadku ciasteczek pięćdziesięciogramowych różnica 3 gram jest odpowiednio mniejsza w stosunku do całego ciasteczka (współczynnik zmienności to 6% i oznacza małe zróżnicowanie populacji).
5. Rozstęp
\(R=X_{max}-X_{min}\)Przypominam, że rozstęp to różnica pomiędzy najwyższą a najniższą wartością cechy. Jest bardzo wrażliwy na wartości skrajne, nietypowe.
6. Rozstęp ćwiartkowy = kwartylny
\(IQR=Q_{3}-Q_{1}\)Jest to miara, która sporo mówi o populacji, gdyż w tych granicach mieści się 50% (czyli dokładnie połowa) badanych obiektów. Im większy rozstęp kwartylny, tym bardziej zróżnicowana jest cecha statystyczna.
7. Odchylenie ćwiartkowe
\(Q=\frac{IQR}{2}=\frac{Q_{3}-Q_{1}}{2}\)Odchylenie ćwiartkowe to połowa rozstępu kwartylnego. Używa się go między innymi do obliczeń pozycyjnego współczynnika zmienności.
PS. To mam nadzieję, że mi się udało wytłumaczyć na czym polega rozproszenie w statystyce. Myślicie, że sierżant również zdołał wyjaśnić, na czym polega rozproszenie w paprociach?
Droga Czytelniczko! Drogi Czytelniku!
Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.
Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.
A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.
Pozdrawiam Cię serdecznie i życzę miłego dnia!
Krystyna Piątkowska