Czy statystyk musi umieć rysować? Czy histogram służy do opowiadania historii? Excel, R, czy może kartka papieru? Po co w ogóle robić wykresy? Tego wszystkiego dowiecie się z dzisiejszego tekstu o histogramach.
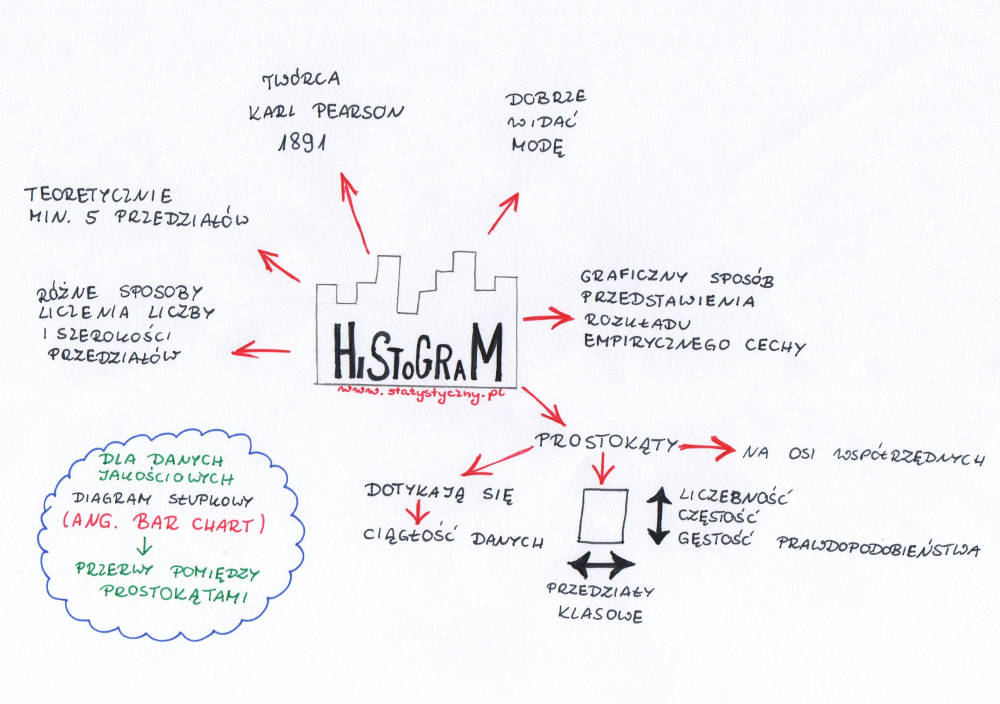
Zacznijmy od definicji: „Histogram to jest graficzny sposób przedstawienia rozkładu empirycznego cechy.” Tak, znowu jakaś skomplikowana regułka, która ma wszystkim udowodnić, że statystyka nie jest dla zwykłych szaraczków, tylko dla wybrańców, którzy takie regułki są w stanie rozszyfrować. No to zastanówmy się, o co w tym jednym zdaniu chodzi. Najlepiej na przykładzie. Graliście kiedyś w Race For The Galaxy? W swoim czasie była to jedna z moich ulubionych gier planszowych i jak tylko uzyskałam możliwość walki „z komputerem”, to spędziłam wiele godzin grając z wirtualnym przeciwnikiem. A ponieważ jestem trochę świrnięta, to przez jakiś czas notowałam sobie wszystkie wyniki. Myślę, że teraz się przydadzą, żeby pokazać przykład budowania histogramu. Zastanówmy się więc, co będziemy badać? Badaną cechą będzie liczba punktów zdobytych przeze mnie w podczas gry w RFTG (pamiętacie, co to populacja i badana cecha? Jeśli nie, przypomnijcie sobie wpis na ten temat, może ułatwić zrozumienie tego tekstu). Rozkład empiryczny, to rozkład na podstawie zanotowanych przeze mnie wyników poszczególnych gier. Co należy z tym zrobić? Wyobraźmy sobie, że histogram to taki wykresik, który przedstawia połączone ze sobą prostokąty. Prostokąty umieszczone są w układzie współrzędnych, gdzie na osi odciętych mamy badaną cechę – w naszym przypadku zdobyte przeze mnie punkty w RFTG (podzielone na kilka przedziałów). Na osi rzędnych mamy natomiast liczebność każdego przedziału.
przykład RFTG
Spróbujmy krok po kroku narysować histogram. Zanotowane mam 50 wyników gier: 34, 28, 29, 21, 28, 26, 22, 22, 27, 27, 37, 21, 35, 23, 34, 21, 30, 33, 21, 25, 20, 27, 25, 21, 23, 32, 34, 36, 29, 16, 21, 20, 35, 31, 22, 23, 20, 30, 28, 21, 33, 29, 23, 18, 24, 24, 27, 55, 37, 33.
Zróbmy z tego szereg przedziałowy, notując ile wyników wystąpowało w każdym przedziale. Rezultat takich obliczeń przedstawia poniższa tabela:
| liczba punktów | liczebność |
| 16-20 | 5 |
| 21-25 | 18 |
| 26-30 | 13 |
| 31-35 | 10 |
| 36-40 | 3 |
| 41-45 | 0 |
| 46-50 | 0 |
| 51-55 | 1 |
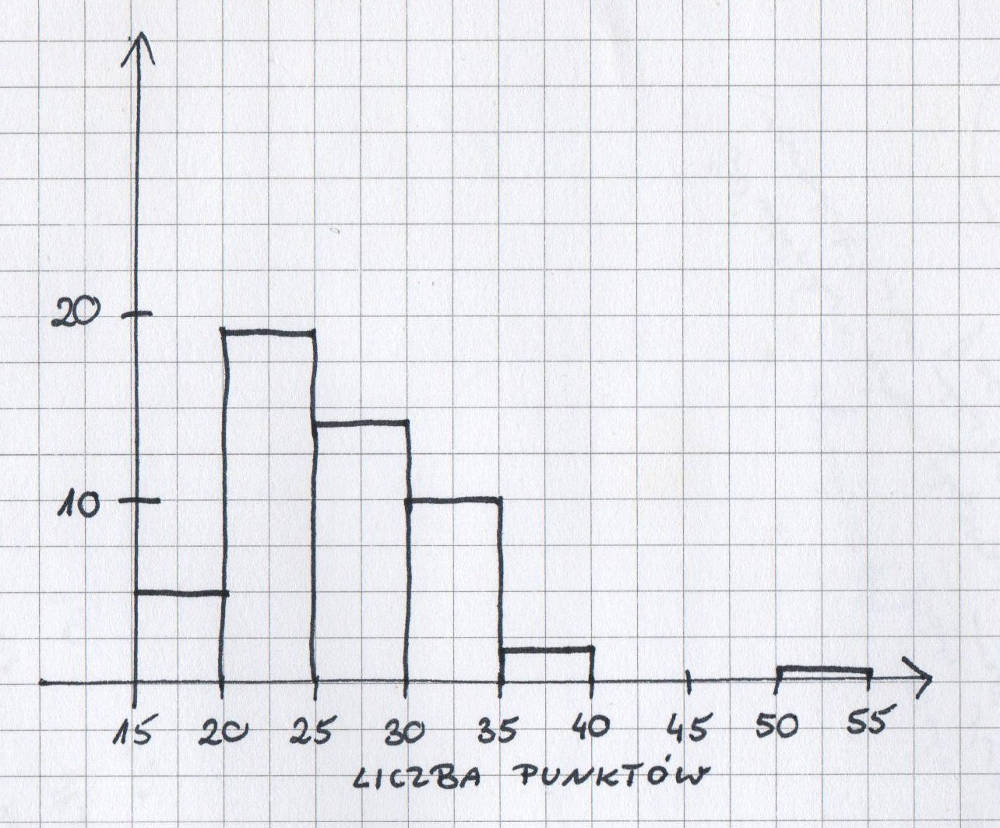
A teraz możemy przenieść wyniki na wykres. Na osi odciętych zaznaczamy nasze przedziały, natomiast na osi rzędnych ich liczebności:
I, proszę bardzo, okazuje się, że prosty histogram bez problemu możemy od ręki narysować w 5 minut (naprawdę, możecie sprawdzić, że więcej czasu na to nie potrzeba).
Taki sam wykres otrzymamy poprzez użycie funkcji hist() w R (w tym przypadku nawet 5 minut nie będzie potrzebne):
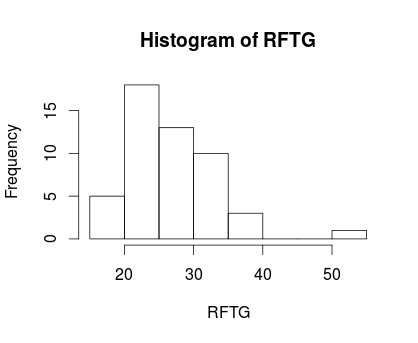
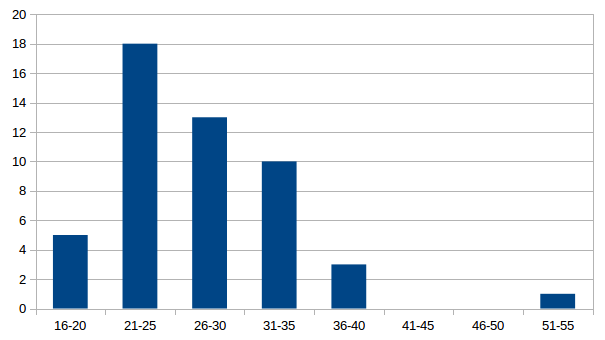
Możemy, oczywiście, skorzystać z arkusza kalkulacyjnego typu Excel (którego użycie jest już bardziej skomplikowane niż wpisanie funkcji w R):
Po co nam histogram?
Po co się bawić w takie rysunki? Czy nie wystarczy samo wyliczenie średniej arytmetycznej, odchylenia standardowego i jeszcze kilku innych wskaźników statystycznych?
Rzecz w tym, że nie zawsze te wskaźniki przekazują pełną informację o badanej populacji. Często warto zobaczyć na rysunku, jak dokładnie wygląda rozkład badanej cechy. Poniżej przedstawiam przykład z rewelacyjnego podręcznika do statystyki (który sama właśnie czytam) OpenIntro Statistics. Mamy do czynienia z trzema różnymi populacjami, w których średnia arytmetyczna wynosi 0, a odchylenie standardowe to 1. Jeśli spojrzycie na rysunek, to już będziecie wiedzieć, jakie różnice między tymi trzema populacjami występują (mimo że podstawowe klasyczne miary położenia i rozkładu są identyczne).
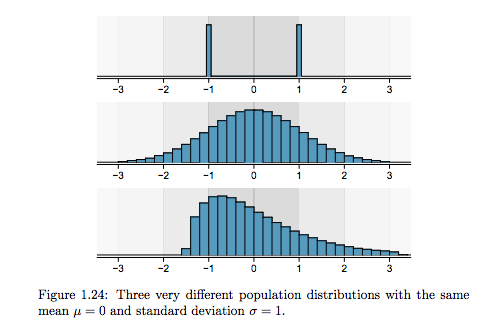
źródło: OpenIntro
Dodatkowe uwagi
Przy konstrukcji histogramu należy zwrócić uwagę na parę ważnych cech. Przede wszystkim pamiętajmy, że nie ma czegoś takiego jak jedyna słuszna liczba przedziałów klasowych, czy jedyna słuszna szerokość takiego przedziału. Są różne sposoby liczenia optymalnej liczby przedziałów, z których każdy różni się między sobą i daje inne wyniki. Niestety, wygląd histogramu można mocno zmienić manipulując szerokością przedziałów. Jest to pole popisu dla nieuczciwych albo niedouczonych statystyków. Dzięki temu optycznie dane mogą wyglądać tak, jak byśmy chcieli, podczas gdy w rzeczywistości są one zupełnie inne. Niezorientowany obserwator może przez to wyciągać błędne wnioski statystyczne.
Dobry histogram to taki, w którym przedziałów jest jak najwięcej, ale równocześnie unika się pustych klas (czyli takich przedziałów, w którym nie występują żadne zaobserwowane wartości). Teoretycznie minimalna liczba przedziałów w histogramie to 5, ale zdarzają się sytuacje, w których zasada ta zostaje złamana.
Pamiętajmy również, że kiedy rysujemy histogram, poszczególne prostokąty powinny się stykać między sobą. Podkreśla to ciągłość danych (gdybyśmy mieli do czynienia z danymi jakościowymi, to moglibyśmy zbudować bardzo podobny wykres – zwany diagramem słupkowym albo z angielskiego „bar chart” – dla rozróżnienia typu cechy poszczególne prostokąty w tym przypadku nie powinny się stykać ze sobą).
Przykład średniego wynagrodzenia
A teraz łamiąc wszelkie zasady budowania histogramów (słyszałam, że zasady są po to, żeby je łamać), chciałam pokazać wykresy dla naszych czterech (analizowanych już wielokrotnie) firm. Dlaczego łamiąc zasady? Bo obserwacji w tym przypadku jest na tyle mało, że nie da się zbudować histogramów, w których by występowało za każdym razem przynajmniej 5 przedziałów. Myślę jednak, że warto zobaczyć, jak optycznie prezentują się wynagrodzenia w poszczególnych firmach. Na etapie nauki warto analizować wszystkie możliwe sposoby prezentacji i analizy danych, żeby potem wybierać te, które będą najlepsze w danej sytuacji.
Poniższe histogramy zostały przygotowane w R. Pozwoliłam na to, żeby program na podstawie danych sam dopasował odpowiednie przedziały.
Na początku przypomnijmy sobie wszelkie informacje na temat wynagrodzenia w analizowanych czterech firmach:
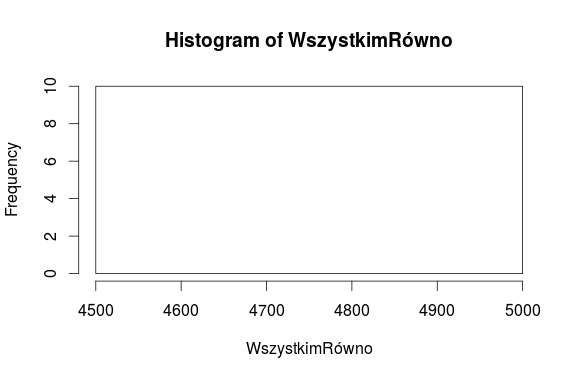
- „Wszystkim Równo” – zatrudnia 10 pracowników, z których każdy dostaje co miesiąc 5000 zł.
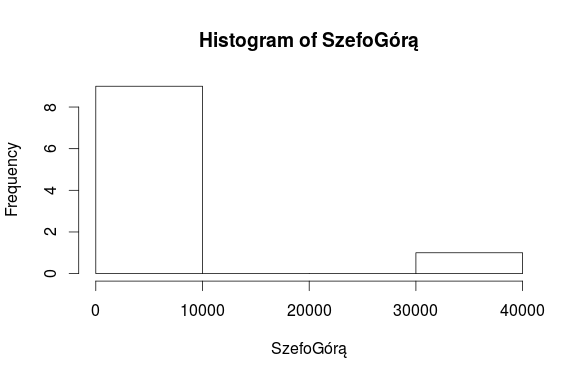
- „Szefo Górą” – zatrudnia panią sprzątaczkę, która na umowę zlecenie otrzymuje 500 zł, do tego 8 szeregowych pracowników z pensją 1500 zł i kierownika, który co miesiąc na konto przyjmuje 37500 zł.
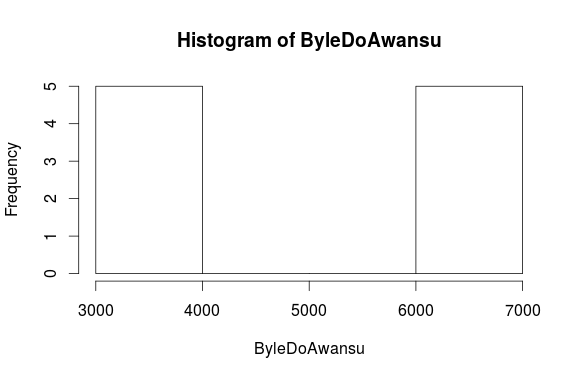
- „Byle do Awansu” – mamy tu również 10 pracowników – pięciu pracuje poniżej roku i otrzymują 3000 zł, druga piątka ma już dłuższy staż i dzięki temu doczekała się pensji po 7000 zł.
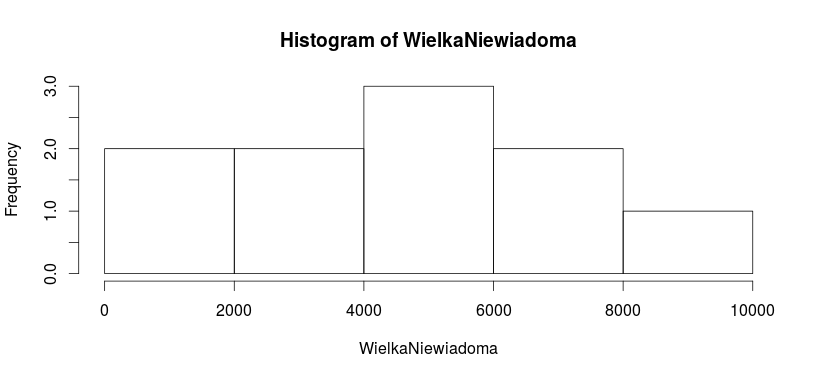
- „Wielka Niewiadoma” – dziesięciu pracowników, każdy z inną pensją, od 1000 do 9000 zł.
A jak wyglądają histogramy. Proszę popatrzeć:
W przypadku firmy „Wszystkim Równo” mamy identyczne zarobki dla wszystkich pracowników. Nic więc dziwnego, że histogram składa się z jednego wielkiego prostokąta, który zawiera wszystkich dziesięć obserwacji.
W przypadku firmy „Szefo Górą” wynagrodzenie szefa istotnie odbiega od pozostałych 9 wynagrodzeń. W związku z tym 9 wynagrodzeń zawiera się w pierwszym przedziale (do 10000 zł), a wynagrodzenie szefa mieści się w przedziale 30000 zł – 40000 zł. Niższe wynagrodzenie sprzątaczki jest w tym samym przedziale co wynagrodzenia większości pracowników, ponieważ różnica 1000 zł jest niewielka w porównaniu z różnicą 36000 zł.
W firmie „Byle do Awansu” wynagrodzenie mogło wynosić albo 3000 zł albo 7000 zł. Wyraźnie widać na histogramie, że mamy dwa prostokąty, które pokazują, że liczność obu przedziałów wynosi dokładnie 5.
W przypadku firmy „Wielka Niewiadoma” mieliśmy do czynienia z różnymi wynagrodzeniami w przedziale 1000 zł do 9000 zł. Histogram jest więc najbardziej zróżnicowany – tak jak najbardziej zróżnicowane były pensje pracowników.
Podsumowanie
Mam nadzieję, że powyższy wpis pomógł Wam zrozumieć, jakie informacje przedstawia histogram. Myślę, że od dzisiaj każdy z Was będzie w stanie narysować własny wykres i w sposób graficzny przedstawić „rozkład empiryczny cechy” (co stawia Was w gronie nielicznych rozumiejących skomplikowane regułki).
W najbliższym czasie planuję przedstawić również inne sposoby prezentacji graficznej danych. Zapraszam do lektury.
Droga Czytelniczko! Drogi Czytelniku!
Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.
Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.
A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.
Pozdrawiam Cię serdecznie i życzę miłego dnia!
Krystyna Piątkowska