Witajcie wszyscy ex-wyznawcy Latającego Potwora Spaghetti, którzy zrozumieliście istotę korelacji pomiędzy liczbą piratów a globalnym ociepleniem. Witajcie wszyscy, którzy chcecie podążyć ścieżką wyznaczoną przez Tylera Vigena i samodzielnie szukać najbardziej nietypowych korelacji. Witajcie wszyscy, którzy nie chcecie drżeć ze strachu na widok skomplikowanego wzoru na współczynnik korelacji Pearsona. Dzisiejszy wpis jest właśnie dla Was.

Mieliśmy okazję zmierzyć się ostatnio z teorią na trudny temat, jakim jest współczynnik korelacji Pearsona. Opisywałam jego wady, zalety i sposoby wykorzystania. Tłumaczyłam różnice pomiędzy korelacją i przyczynowością. Pokazywałam, jak łatwo wykorzystać korelację, żeby przekonać do czegoś kogoś, kto nie ma nic wspólnego ze statystyką. Dziś pora na prezentację, jak obliczyć współczynnik korelacji Pearsona krok po kroku.

przykład obliczeń – wiek a liczba dzieci

Zacznijmy od prostego przykładu z konkretnymi danymi. Mamy firmę, która zatrudnia 13 kobiet. Chcemy się dowiedzieć, czy wiek tychże kobiet jest skorelowany w jakikolwiek sposób z liczbą posiadanych przez nie dzieci. Wiadomo, można skorzystać z gotowców w arkuszach kalkulacyjnych czy programach statystycznych, ale czasem zdarzają się takie sytuacje, kiedy jednak trzeba umieć samodzielnie wykorzystać wzór i zrobić obliczenia krok po kroku. Jeśli patrząc na wzór z kilkoma sumami, pierwiastkiem i dziwnymi iloczynami, odczuwasz strach, to nie jesteś odosobniony. Ale nie martw się. Zaraz pokażę, jak się z nim zmierzyć.

\(r_{xy}=\frac{\sum_{i=1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}\sum_{i=1}^{n}(y_{i}-\overline{y})^{2}}}\)

Wzór ten wygląda tak nieciekawie, że sama za pierwszym razem byłam przygotowana, że gdzieś po drodze się pomylę. Jakie było zaskoczenie, kiedy wyliczony ręcznie współczynnik korelacji okazał się dokładnie taki sam, jak wyliczony za pomocą odpowiedniej funkcji. I okazało się, że wcale nie jest to takie trudne. Spróbuję więc pokazać tutaj krok po kroku, jak najprościej można samemu policzyć współczynnik korelacji Pearsona. Zrobimy tabelkę, która pomoże nam trochę w tych obliczeniach. W pierwszej kolumnie wpiszemy wiek kobiety (x), a w drugiej kolumnie znajdzie się liczba jej dzieci (y):

wiek kobiety (x)	liczba dzieci (y)
55	5
21	1
35	2
58	2
28	1
30	2
32	3
20	0
35	0
46	0
34	2
53	0
30	4

Na początku trzeba wyliczyć średnią arytmetyczną wieku kobiet (\(\overline{x}\)) i średnią arytmetyczną liczby dzieci (\(\overline{y}\)). Jest to odpowiednio 36,69 i 1,69. Następnie do tabelki dodajemy nową kolumnę i wpisujemy do niej obliczoną różnicę pomiędzy wiekiem danej kobiety i średnią wieku kobiet w naszym zakładzie pracy (\(x_{i}-\overline{x}\)).

Pierwsza kobieta: 55 – 36,69 = 18,31

Druga kobieta: 21 – 36,69 = -15,69

I tak po kolei dla wszystkich kobiet.

wiek kobiety (x)	liczba dzieci (y)	\(x_{i}-\overline{x}\)
55	5	18.31
21	1	-15.69
35	2	-1.69
58	2	21.31
28	1	-8.69
30	2	-6.69
32	3	-4.69
20	0	-16.69
35	0	-1.69
46	0	9.31
34	2	-2.69
53	0	16.31
30	4	-6.69

Następnie to samo robimy dla liczby dzieci (\(y_{i}-\overline{y}\)). Zaczynamy od pierwszej kobiety: 5 – 1,69 = 3,31 i kontynuujemy do końca tabelki:

wiek kobiety (x)	liczba dzieci (y)	\(x_{i}-\overline{x}\)	\(y_{i}-\overline{y}\)
55	5	18.31	3.31
21	1	-15.69	-0.69
35	2	-1.69	0.31
58	2	21.31	0.31
28	1	-8.69	-0.69
30	2	-6.69	0.31
32	3	-4.69	1.31
20	0	-16.69	-1.69
35	0	-1.69	-1.69
46	0	9.31	-1.69
34	2	-2.69	0.31
53	0	16.31	-1.69
30	4	-6.69	2.31

Następnie mnożymy przez siebie dane z trzeciej i czwartej kolumny, a także obliczamy kwadraty dla trzeciej i czwartej kolumny:

wiek kobiety (x)	liczba dzieci (y)	\(x_{i}-\overline{x}\)	\(y_{i}-\overline{y}\)	\((x_{i}-\overline{x})*(y_{i}-\overline{y})\)	\((x_{i}-\overline{x})^{2}\)	\((y_{i}-\overline{y})^{2}\)
55	5	18.31	3.31	60.56	335.17	10.94
21	1	-15.69	-0.69	10.86	246.25	0.48
35	2	-1.69	0.31	-0.52	2.86	0.09
58	2	21.31	0.31	6.56	454.02	0.09
28	1	-8.69	-0.69	6.02	75.56	0.48
30	2	-6.69	0.31	-2.06	44.79	0.09
32	3	-4.69	1.31	-6.14	22.02	1.71
20	0	-16.69	-1.69	28.25	278.63	2.86
35	0	-1.69	-1.69	2.86	2.86	2.86
46	0	9.31	-1.69	-15.75	86.63	2.86
34	2	-2.69	0.31	-0.83	7.25	0.09
53	0	16.31	-1.69	-27.60	265.94	2.86
30	4	-6.69	2.31	-15.44	44.79	5.33

W następnym kroku musimy zsumować te trzy świeżo obliczone kolumny.

Pierwsza: \(\sum_{i=1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})=46,77\)

Druga: \(\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}=1866,77\)

Trzecia: \(\sum_{i=1}^{n}(y_{i}-\overline{y})^{2}=30,77\)

Na koniec zostaje ostateczne podstawienie do wzoru:

\(r_{xy}=\frac{46,77}{\sqrt{1866,77*30,77}}=0,195\)

Obliczenia nie okazały się aż tak trudne. A wniosek jest prosty – w naszym zakładzie pracy brak korelacji pomiędzy wiekiem kobiet i liczbą ich dzieci.

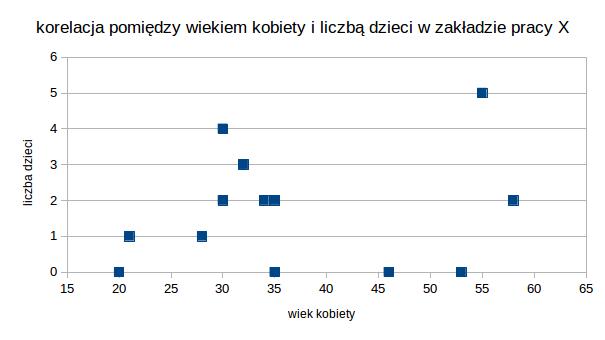
Możemy sobie to również obejrzeć na wykresie:

Nie tylko z obliczeń, ale również na wykresie widać wyraźnie, że żadna korelacja nam się nie chce wyrysować.

przykłady korelacji dla polskich województw

Teraz już bez konkretnych obliczeń – trochę wykresów i danych z życia, a właściwie z roczników statystycznych wziętych.

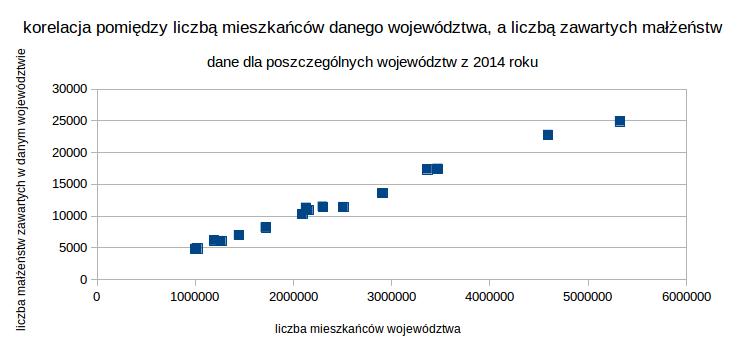
Zaczęłam od liczby mieszkańców poszczególnych województw i liczby zawartych małżeństw w danym województwie. Nie zdziwiłam się bardzo, widząc wysoką wartość współczynnika korelacji Pearsona r=0,99. Kiedy narysowałam sobie wykres – poszczególne punkty układały się niemalże jak na linii prostej. Zdecydowanie korelacja jest bardzo wysoka.

Myślałam, że podobnie wysoka korelacja będzie również dla takich cech jak powierzchnia województwa i liczba zamieszkujących je osób. Okazało się jednak, że współczynnik korelacji Pearsona wyniósł zaledwie r=0,47. Jest to wartość, która wskazuje na bardzo umiarkowaną korelację. Wykres również wygląda zupełnie inaczej niż poprzedni: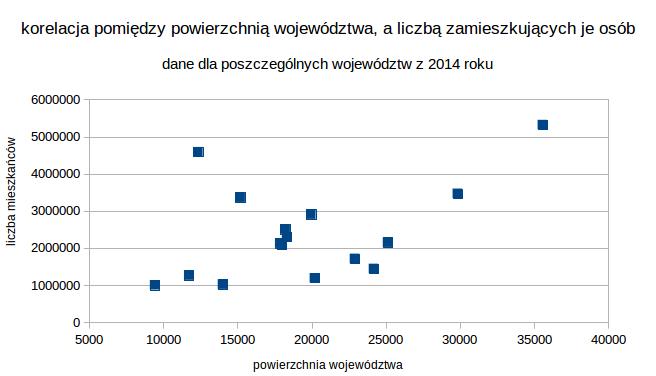

Ponieważ wyszukiwanie danych na stronie GUS było dość uciążliwe, postanowiłam kolejne poszukiwania ciekawych korelacji robić nie na podstawie województw, ale poszczególnych państw unijnych.

przykłady korelacji dla poszczególnych państw z UE

W związku z tym przeniosłam się na stronę eurostat (taki europejski odpowiednik naszego GUS) i tam przejrzałam mnóstwo przeróżnych zestawień. Na ich podstawie porobiłam wykresy, policzyłam współczynniki korelacji. Kilka ciekawych przykładów przedstawiam poniżej.

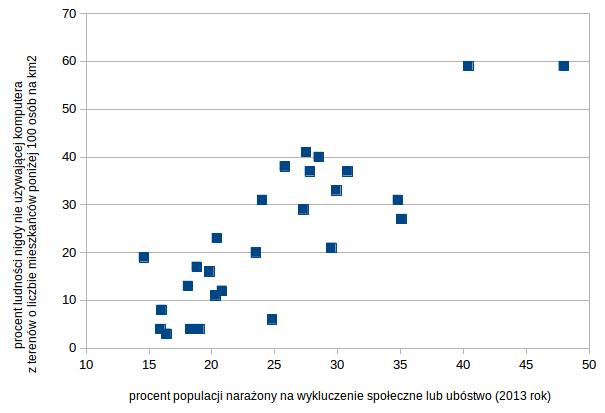
Pierwszy przykład, w którym wysoki współczynnik korelacji Pearsona r= 0,84 wydaje się być bardzo logiczny. Na wykresie procent populacji narażony na wykluczenie społeczne lub ubóstwo i jego korelacja z procentem ludności z terenów małozaludnionych (takich gdzie na kilometr kwadratowy nie ma nawet 100 mieszkańców), którzy nigdy w życiu nie korzystali z komputera.

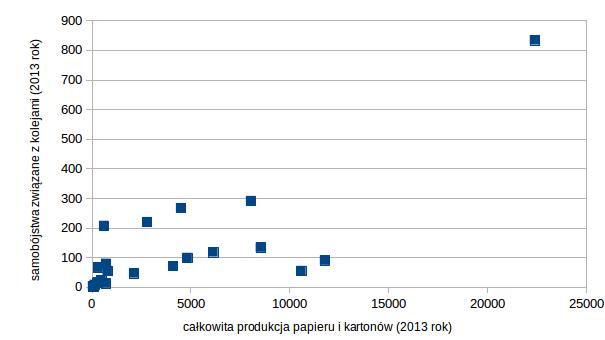
Drugi przykład już nie wydaje się tak bardzo logiczny, pomimo wysokiego współczynnika korelacji r=0,79. Przedstawiam na osi x całkowitą produkcję papieru i kartonów w 2013 roku, a na osi y samobójstwa powiązane z kolejami. Zauważyć można, że duży wpływ na taką wartość współczynnika korelacji ma jedna obserwacja (zainteresowanych informuję, że są to Niemcy), gdzie mamy do czynienia zarówno z dużą liczbą samobójstw kolejowych jak i wysoką produkcją papieru.

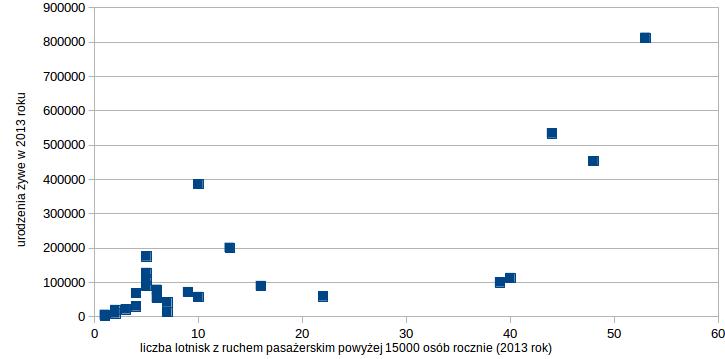
I znów wysoki współczynnik korelacji tam, gdzie byśmy się go nie spodziewali. Wynosi on r=0,75, a dotyczy korelacji pomiędzy liczbą lotnisk z ruchem pasażerskim powyżej 15000 osób rocznie, a urodzeniami żywymi w danym kraju. Korelacja wysoka, być może dlatego, że w większych i bardziej zaludnionych państwach mamy zarówno więcej lotnisk jak i większą szansę na liczne potomstwo.

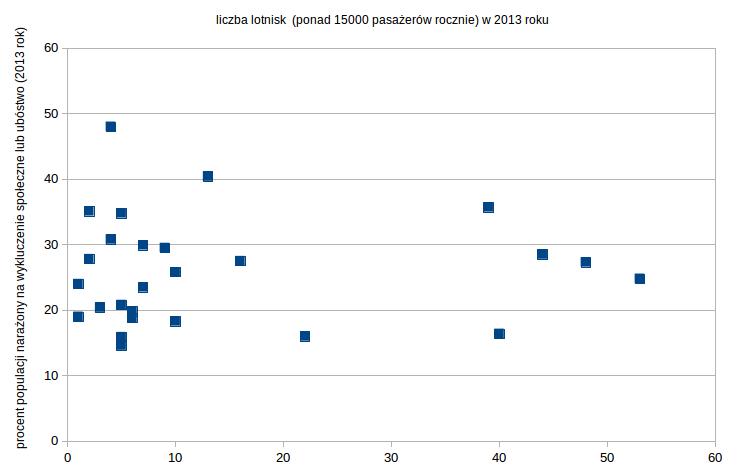
A tu przykład całkowitego braku korelacji. Współczynnik Pearsona wynosi zaledwie r=0,01. Brak jakiegokolwiek powiązania pomiędzy liczbą lotnisk, a procentem populacji narażonym na wykluczenie społeczne lub ubóstwo.

I na tym chwilowo chciałam zakończyć moje przykłady związane z współczynnikiem korelacji Pearsona. Mam nadzieję, że już dla nikogo temat ten nie jest straszny. A jeśli ktoś z czytelników również pokusił się o jakieś obliczenia, wykresy, analizy, to zapraszam do podzielenia się obserwacjami.

---

Droga Czytelniczko! Drogi Czytelniku!

Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.

Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.

A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.

Pozdrawiam Cię serdecznie i życzę miłego dnia!

Krystyna Piątkowska