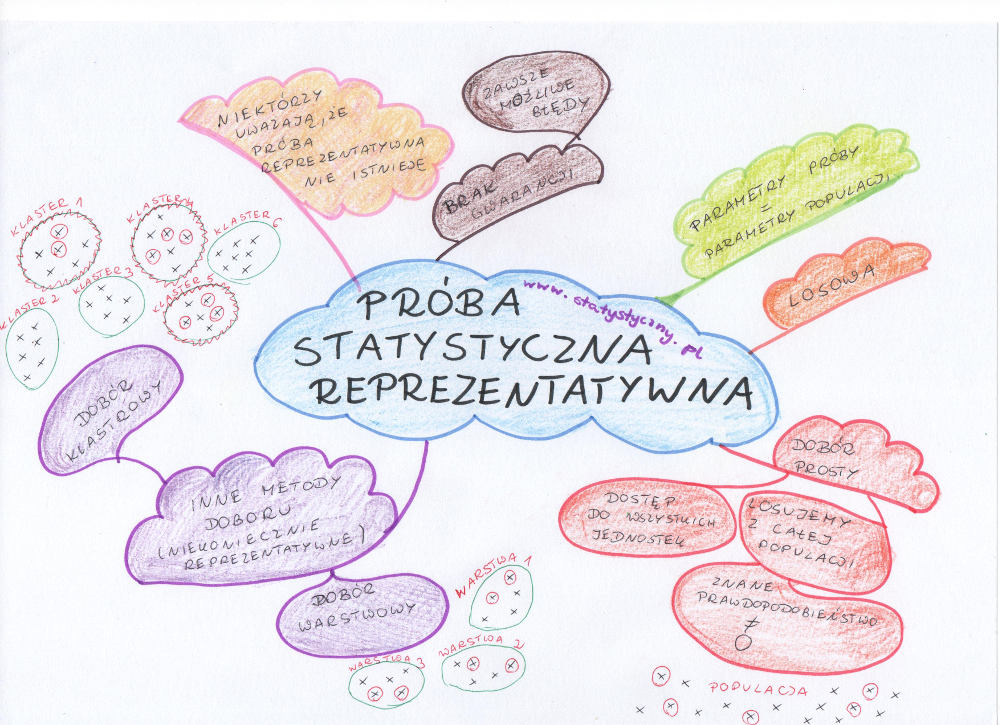
W poprzednim artykule o próbie statystycznej porównywałam badanie statystyczne do próbowania gulaszu. Wspominałam, że losując elementy z populacji próbujemy właśnie w podobny sposób oszacować parametry dla całej populacji, opierając się tylko na niewielkim wycinku całości. Żeby je oszacować – musimy stworzyć tzw. próbę reprezentatywną. Powinna ona odpowiadać cechom całej populacji (za wyjątkiem liczebności). Czyli wyliczona średnia arytmetyczna dla próby ma być zbliżona do średniej arytmetycznej całej populacji. Obliczone odchylenie standardowe ma być zbliżone do odchylenia standardowego populacji. Podobnie wyszystkie inne miary rozkładu. Niektórzy twierdzą, że nie da się stworzyć takiej próby, którą moglibyśmy nazwać reprezentatywną. Wciąż jednak termin ten jest bardzo popularny i choć trudno trafić na zbiór idealnie odwzorowujący populację, to zwykle udaje nam się całkiem dobrze przybliżyć parametry rozkładu, jeśli mamy do czynienia z dobrze dobraną próbą.
Co zrobić, żeby powstała reprezentatywna próba statystyczna?
Najprościej stworzyć próbę reprezentatywną, kiedy mamy łatwy dostęp do wszystkich jednostek w populacji. Wtedy w sposób losowy wybieramy określoną przez nas liczbę jednostek (liczba zależy od tego, na ile dokładne wyniki chcielibyśmy otrzymać) i możemy zacząć wykonywanie obliczeń. Pamiętajmy, że wybór jednostek do próby powinien być absolutnie losowy, nie sterowany przez nas w żaden sposób. Czyli nie że co piąta osoba albo ankieta rozdana wśród znajomych. Trzeba zrobić listę wszystkich jednostek i wylosować te, które wejdą w skład naszej próby.
Nie będą reprezentatywne:
- numery z książki telefonicznej (bo można mieć numer zastrzeżony)
- co dziesiąty student przed uczelnią (bo różne grupy o różnych godzinach kończą zajęcia)
- co siódmy dzień tygodnia (bo zawsze będzie to ten sam dzień)
- sondy internetowe (bo odpowiadają tylko użytkownicy internetu, zainteresowani tematem)
- ankiety w tv (bo odpowiadają tylko widzowie danego programu, którzy lubią brać udział w takich ankietach)
- co dwudziesta czekolada zdjęta z taśmy produkcyjnej (bo być może właśnie co dwudziesta czekolada waży mniej albo więcej od pozostałych i trafia do niej więcej rodzynek)
Przy tym wszystkim trzeba pamiętać, że nawet jeśli zrealizujemy wszystkie możliwe postulaty, wylosujemy idealne jednostki, wszystko będzie niezależne, wszystko zgodnie ze sztuką statystyczną – próba jest tylko próbą. Zawsze może się okazać, że mamy do czynienia z błędami i średnia z próby a średnia z populacji różnią się więcej niż teoretyczny błąd statystyczny.
Metody losowania jednostek do próby statystycznej
Oprócz prostego losowania jednostek do próby statystycznej stosowane są również inne metody. Opowiem tutaj krótko o dwóch z nich, a być może kiedyś jeszcze wrócimy do tematu bardziej szczegółowo.
- Dobór warstwowy – mamy tu do czynienia z podziałem populacji na warstwy na podstawie podobieństwa jednostek. Z każdej warstwy następnie pobieramy określoną liczbę jednostek. Najprostszy podział na dwie warstwy to podział badanych ludzi wg płci (czyli mamy warstwę kobiet i warstwę mężczyzn). Można dzielić też ludzi na podstawie dochodów, koloru skóry, wzrostu – zależy na jakim podziale warstwowym nam zależy. Uwaga! Przy takim doborze próby okazuje się, że nie wszystkie metody analizy można stosować tak, jak przy prostym losowaniu z populacji.
- Dobór klastrowy – dzielimy populację, ale nie na podstawie podobieństwa jednostek, ale np. na podstawie położenia geograficznego. Załóżmy, że chcemy przeanalizować mieszkańców wsi w Polsce. Gdybyśmy wylosowali mieszkańców ze wszystkich wsi, to badacze musieliby sporo podróżować, żeby każdego z nich spotkać. Dobór klastrowy pozwala na losowy wybór określonej liczby wsi i tylko z tych wsi następnie losuje się badane jednostki. Taki sposób zwiększa ryzyko błędów (bo jeśli wylosują się raczej bogatsze wsie, to informacje o ich mieszkańcach nie będą odzwierciedlać danych dla mieszkańców wsi z całej Polski), ale równocześnie pozwala zredukować koszty. Jeśli nie mamy możliwości dokonać losowania z całej populacji, to podział na klastry może być najlepszym rozwiązaniem. Pamiętać jednak należy o większym ryzyku popełnienia błędów i stosować odpowiednie metody do obliczeń.
Zarówno metoda prostego losowania, jak i dobór warstwowy czy klastrowy, opierają się na rachunku prawdopodobieństwa. Każda jednostka z określonym prawdopodobieństwem będzie mogła znaleźć się w naszej próbie statystycznej. Prawdopodobieństwo to powinno być znane i różne od 0.
Pamiętajmy, że są również metody badań statystycznych, które zakładają celowy i świadomy dobór jednostek do próby. Są one zwykle wykorzystywane w innym celu niż badanie parametrów populacji. Mają swoje wady i zalety. Należy jednak pamiętać, że w takiej sytuacji na pewno nie będziemy mieć do czynienia z próbą reprezentatywną (nie zawsze reprezentatywna próba statystyczna jest nam potrzebna).
Zapraszam na fanpage bloga: blog statystyczny na facebooku.
Droga Czytelniczko! Drogi Czytelniku!
Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.
Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.
A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.
Pozdrawiam Cię serdecznie i życzę miłego dnia!
Krystyna Piątkowska