Dziś bardziej praktycznie. Czyli krótka analiza statystyczna. Czyli przykład. Czyli liczba moich własnych kroków w pierwsze 41 dni używania opaski zliczającej. Będą wykresy, będą obliczone poszczególne miary, będzie trochę wniosków. Zapraszam do czytania.
Na początku musimy sprawdzić, ile kroków wykonałam przez wspomniane 41 dni. Dane pochodzą ze specjalnej opaski analizującej moją aktywność fizyczną. Tak wygląda liczba kroków z poszczególnych dni:
9216, 7061, 5103, 11730, 9990, 6484, 11022, 9198, 6360, 8049, 6816, 9361, 9552, 10079, 9540, 8737, 8227, 8348, 8047, 17610, 9528, 9583, 8616, 8183, 8270, 11369, 19174, 8106, 8571, 8339, 5201, 10007, 11482, 8148, 9228, 10077, 11315, 8337, 8881, 12899, 13187.
Czy można to jakoś przeanalizować, czy można wyciągnąć jakiekolwiek wnioski?
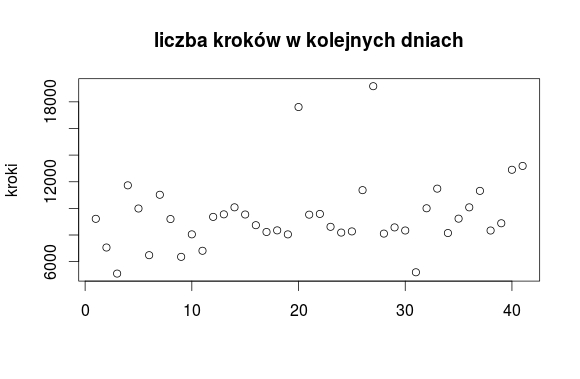
Zacznijmy może od wykresu:
Miary położenia i rozproszenia
Tak oto wyglądało moje wędrowanie. Raz więcej tych kroków, raz mniej. Spróbujmy jednak wyciągnąć jakieś bardziej konkretne informacje. Może obliczymy średnią arytmetyczną? Suma wszystkich kroków wyniosła 38903, a dni było 41. Po podzieleniu daje nam to wynik 9489 kroków dziennie (przy zalecanym poziomie 8000 kroków każdego dnia, wynik jest całkiem zadowalający, choć staram się go poprawić).
Następnie liczę odchylenie standardowe. Można użyć dowolnego programu obliczającego, albo pomęczyć się samemu krok po kroku. Moje odchylenie standardowe to 2675 kroków (pamiętacie, że odchylenie standardowe ma taką samą jednostkę jak badana cecha?).
Jak już mamy średnią i ochylenie standardowe, to pora na współczynnik zmienności. Jak to jest? Czy chodzę zawsze regularnie tyle samo kroków każdego dnia, czy raczej raz więcej raz mniej?
Obliczmy: \(V=\frac{2675}{9489}*100\%=28,19\%\)
Czyli co? Czyli mamy średnie zróżnicowanie w populacji moich kroków. Wniosek z tego taki, że zdarzają mi się dni bardziej „chodliwe” i bardziej leniwe, ale zróżnicowanie nie jest zbyt duże.
Przejdźmy do miar pozycyjnych. Mody tu nie znajdziemy, nie zdarzyło mi się przez 41 dni zrobić dwa razy tyle samo kroków. Ale na pewno znajdziemy medianę. Wystarczy posortować wszystkie wartości, wybrać środkową i… mamy 9198 kroków. To teraz kwartyle (tak, trzeba wybrać jeden ze sposobów obliczeń, ja zdecydowałam się na pierwszą metodę). 8165,5 oraz 10078 – tyle wynoszą mój pierwszy i trzeci kwartyl liczby kroków. A skoro tyle wynoszą dwa kwartyle, to znaczy, że połowa moich dziennych przejść (przebiegów?) mieści się właśnie w tym przedziale.
W kolejnym kroku możemy obliczyć rozstęp ćwiartkowy (IQR). Odejmujemy od 10078 liczbę 8165,5 i otrzymujemy wynik 1912,5.
Po podzieleniu rozstępu ćwiartkowego na pół dowiadujemy się, że nasze odchylenie ćwiartkowe to Q= 956,25.
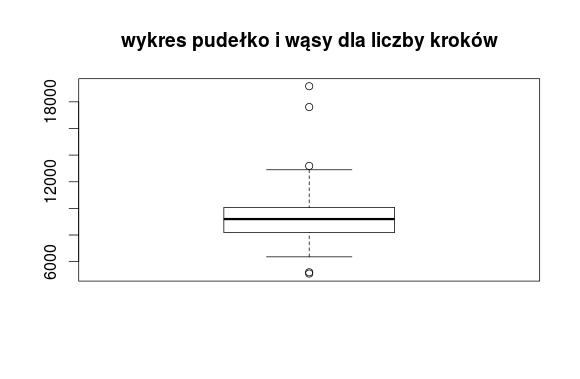
Odchylenie ćwiartkowe i mediana pozwalają nam na obliczenie pozycyjnego współczynnika zmienności: \(V_{Q}=\frac{956,25}{9198}*100\%=10,4\%\). Jest on niższy od klasycznego współczynnika, co może sugerować, że ten pierwszy został zakłócony wartościami skrajnymi. Czy rzeczywiście takie występowały? Zobaczmy to na wykresie pudełko i wąsy.
Troszkę kropek tu występuje. Przypomnijmy, że korzystamy z wykresu Tukeya, na którym kropkami zaznaczaliśmy wartości wychodzące poza półtora wartości rozstępu ćwiartkowego. Są to więc wartości, które dość wyraźnie różnią się od mediany i kwartyli.
Spójrzmy jeszcze na minimum i maksimum. Są to odpowiednio 5103 i 19174. Rozstęp między nimi wynosi 14071. Dość duża wartość, nie uważacie?
Miary asymetrii i koncentracji
To teraz pora na miary asymetrii. Było ich kilka, przeanalizujmy wszystkie po kolei:
Współczynnik asymetrii wynosi 1,64, co sugeruje, że mamy do czynienia z asymetrią prawostronną.
Ze względu na brak mody nie możemy wyznaczyć wskaźnika skośności opartego na modzie. Możemy tylko obliczyć pozycyjny, który wynosi -152,5. Wartości ujemne mówią, że rozkład jest lewostronnie skośny.
Pierwszy współczynnik skośności Pearsona znów potrzebowałby mody, w związku z czym go nie obliczamy.
W kolejce czeka drugi współczynnik skośności Pearsona. Mówi o tym, jaką część odchylenia standardowego stanowi różnica pomiędzy średnią arytmetyczną a medianą. Wartość tę mnoży się przez 3. W przypadku moich kroków wynosi on 0,33 i wskazuje na asymetrię prawostronną.
I jeszcze współczynnik Bowley’a oparty na kwartylach, który wynosi -0,16 i znowu sugeruje asymetrię lewostronną.
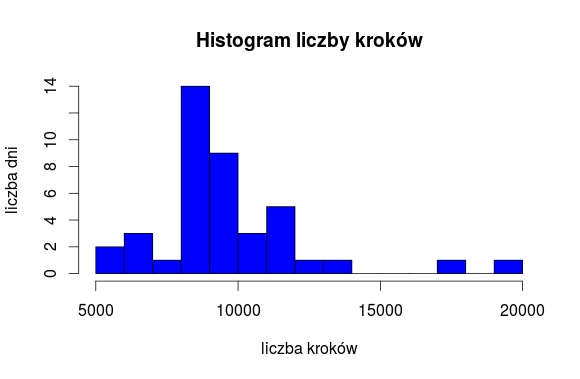
Hmmm… Na pewno zauważyliście, że raz jest dodatnio, raz ujemnie. Skąd te różnice? Dwa współczynniki mówią o asymetrii prawostronnej, dwa mówią o lewostronnej. W tym cały urok statystyki, żeby nie stwierdzić, że obliczenia są bezsensowne, ale żeby zrozumieć, dlaczego odpowiedzi są tak różne. Pamiętajmy, że współczynniki oparte na kwartylach dotyczą wyłącznie jednostek pomiędzy pierwszym i trzecim kwartylem. W związku z tym nie dotyczą ich nietypowe wysokie wartości – a to one „wyciągają” prawe ramię wykresu. Zobaczmy to na histogramie:
Wyraźnie widać, że te parę dni, kiedy osiągnęłam ponadprzeciętnie wysokie wyniki sportowe, ma wpływ na wskaźniki asymetrii. Ale tylko te liczone metodami klasycznymi, a nie na podstawie miar pozycyjnych. Bo miary pozycyjne (kwartyle) nie biorą pod uwagi wartości skrajnych i skupiają się tylko na tym, co najbardziej przeciętne. A „środeczek” wykresu wygląda już bardziej lewostronnie.
Co jeszcze nam zostało? Kurtoza. Wynosi ona 6,93. Przeliczamy od razu eksces odejmując od wyniku 3 i dostajemy 3,93. Wynik większy od 0 więc wniosek, że wykres jest leptokurtyczny. Pamiętacie? Leptokurtyczny to ten, który lepi nam się w górę. Czyli gdybyśmy mieli do czynienia z rozkładem normalnym dla takiej średniej arytmetycznej i odchylenia standardowego, to byłby on bardziej spłaszczony od naszego wykresu.
Ufffff… Kroki przeanalizowane. Mam nadzieję, że taki konkretny przykład uda Wam się wykorzystać do przeróżnych swoich danych. I mam nadzieję, że zauważyliście, że każdą wartość staram się nie tylko obliczyć, ale również zrozumieć. Dlaczego współczynnik asymetrii raz jest dodatni a innym razem ujemny? Dlaczego miary pozycyjne różnią się od klasycznych? Nie wystarczy stwierdzić, że tak jest. Warto jeszcze zakumać dlaczego tak jest i wyciągnąć odpowiednie wnioski.
Droga Czytelniczko! Drogi Czytelniku!
Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.
Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.
A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.
Pozdrawiam Cię serdecznie i życzę miłego dnia!
Krystyna Piątkowska