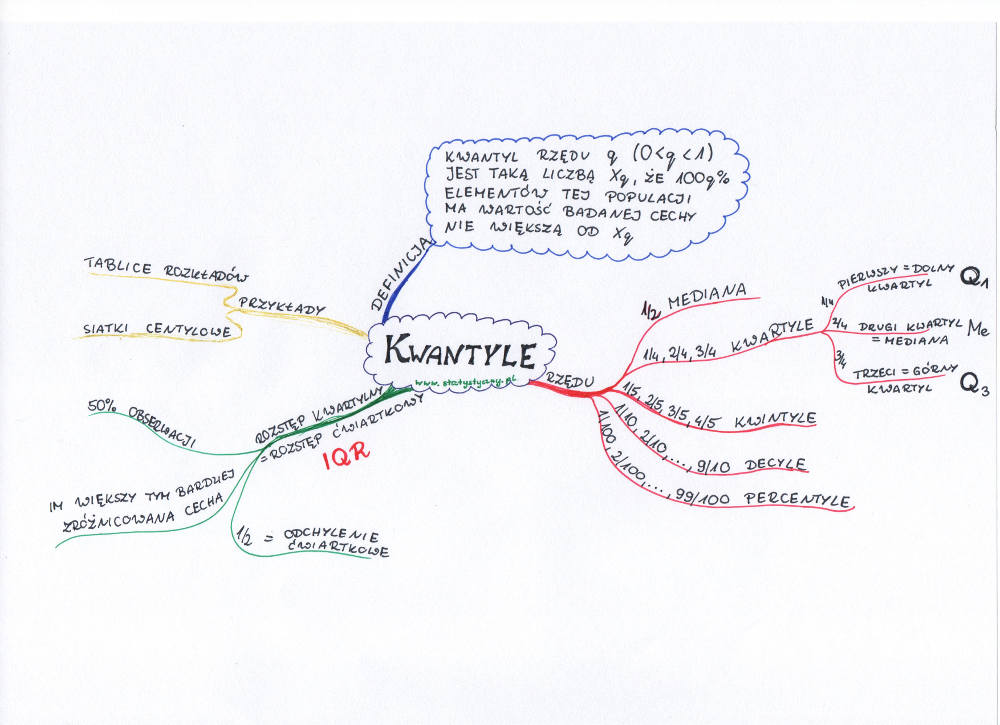
Cóż to jest kwantyl? Zacznijmy znowu od definicji encyklopedycznej, którą zaraz postaram się jak najbardziej przystępnie wytłumaczyć. Według niej kwantyl rzędu q (0 < q < 1) w populacji jest taką liczbą xq, że q*100% elementów tej populacji ma wartość badanej cechy nie większą od xq .Brzmi to strasznie skomplikowanie, prawda?
To spróbujmy w takim razie zobaczyć, co to oznacza dla q=1/2. Kwantyl rzędu 1/2 w populacji to taka liczba, że 50% (100*1/2) elementów tej populacji ma wartość badanej cechy nie większą od x1/2 . Czy z czymś się to Wam kojarzy? Tak, to właśnie jest znana już nam mediana. Oprócz mediany do najbardziej popularnych kwantyli zaliczamy również kwartyle (dzielące populację na cztery części – pierwszy kwartyl, mediana i trzeci kwartyl), kwintyle (czyli kwantyle rzędu 1/5, 2/5, 3/5, 4/5), decyle (dzielące na dziesięć części) oraz percentyle (dzielące populację na 100 części).
Metody obliczania kwartyli
W analizie statystycznej często wykorzystywane są kwartyle. Na pierwszy rzut oka obliczenie kwartyli nie powinno stwarzać żadnych trudności, tymczasem okazuje się dużo bardziej skomplikowane niż byśmy chcieli. Różne źródła podają różne sposoby i trudno znaleźć jedyny słuszny. Poniżej przedstawiam trzy metody obliczania kwartyli – jeśli ktoś spotkał się z jeszcze jakąś inną, to zapraszam do przedstawienia jej w komentarzu.
Metoda pierwsza:
Najpierw wyznaczamy medianę (z wzoru, który już znamy – można sobie przypomnieć w artykule o medianie). Mediana dzieli nam populację na dwa podzbiory, istotnym jest, że mediany nie uwzględniamy w żadnym z podzbiorów. W każdym z nich znów wyznaczamy medianę. Mediana z podzbioru wartości mniejszych od mediany to pierwszy kwartyl. Mediana z podzbioru wartości większych od mediany to trzeci kwartyl.
Metoda druga:
Wyznaczamy medianę i na jej podstawie znów dzielimy populację na dwa podzbiory. Jeśli mieliśmy do czynienia z nieparzystą liczbą obserwacji i mediana jest rzeczywistą wartością środkową (nie musieliśmy obliczać średniej arytmetycznej z dwóch sąsiednich liczb), to w takiej sytuacji uwzględniamy ją w obydwóch podzbiorach. Jeśli liczba obserwacji była parzysta, medianę liczyliśmy jako średnią z dwóch liczb środkowych, to w takiej sytuacji nie uwzględniamy mediany w żadnym podzbiorze. Podobnie jak w pierwszej metodzie, obliczamy mediany dla obu podzbiorów i w ten sposób otrzymujemy pierwszy i trzeci kwartyl.
Metoda trzecia:
W przypadku parzystej liczby obserwacji korzystamy z metody drugiej. Jeśli natomiast liczba obserwacji jest nieparzysta, to sprawa jest dużo bardziej skomplikowana. Liczbę elementów w populacji dzielimy przez 4 i sprawdzamy jaka zostanie nam reszta z dzielenia (może to być 1 lub 3). Załóżmy, że liczba elementów w populacji to N. N=4*n+1 albo 4*n+3 (n to iloraz z dzielenia liczby N przez 4).
- Jeśli mieliśmy do czynienia z 4*n+1 elementów w populacji, to dolny kwartyl liczymy jako 25% z n-tego elementu populacji plus 75% z kolejnego (n+1) elementu. Górny kwartyl natomiast obliczamy poprzez zsumowanie 75% z 3*n+1 elementu populacji oraz 25% z 3*n+2 elementu populacji.
- Jeśli mieliśmy do czynienia z 4*n+3 elementów w populacji, to dolny kwartyl liczymy jako 75% z n+1 elementu populacji plus 25% z kolejnego (n+2) elementu. Górny kwartyl natomiast obliczamy poprzez zsumowanie 25% z 3*n+2 elementu populacji oraz 75% z 3*n+3 elementu populacji.
Przykład – parzysta liczba elementów
Poszczególne metody brzmią strasznie, ale zaraz postaram się je pokazać na jak najprostszych przykładach. Na początku parzysta liczba elementów:
Zaobserwowane dane to: 1, 2, 3, 4, 5, 6
Metoda pierwsza:
Najpierw liczymy medianę jako średnią pomiędzy wartościami 3 i 4, co daje nam wynik 3,5. Otrzymujemy więc dwa podzbiory: 1, 2, 3 oraz 4, 5, 6. W pierwszym podzbiorze mediana wynosi 2 – jest to pierwszy kwartyl. W drugim podzbiorze mediana wynosi 5 – jest to trzeci kwartyl.
Metoda druga:
Mediana wynosi 3,5 i ponieważ była liczona jako wartość średnia pomiędzy dwoma elementami populacji, to nie uwzględniamy mediany w żadnym z podzbiorów i w związku z tym podzbiory wyglądają tak jak w metodzie pierwszej, czyli: 1, 2, 3 oraz 4, 5, 6. Poszczególne kwartyle to 2 i 5.
Metoda trzecia:
Ponieważ mamy do czynienia z parzystą liczbą elementów – obliczenia wyglądają dokładnie tak samo w poprzednich metodach – poszczególne wyniki są identyczne: Me=3,5, Q1=2, Q3=5.
Przykład – nieparzysta liczba elementów
Teraz spróbujmy zrobić to samo dla nieparzystej liczby elementów w populacji. Niech to będzie: 1, 2, 3, 4, 5, 6, 7.
Metoda pierwsza:
Mediana to wartość środkowa, czyli 4. Dzieli ona populację na dwa podzbiory – w żadnym z nich nie jest uwzględana. Oznacza to, że kwartyle liczymy ze zbiorów: 1, 2, 3 oraz 5, 6, 7. Pierwszy kwartyl wynosi 2 (wartość środkowa pierwszego zbioru), trzeci kwartyl wynosi 6 (wartość środkowa drugiego zbioru).
Metoda druga:
Mediana wynosi 4. Ponieważ jest to wartość rzeczywista z populacji, to uwzględniamy ją w obu podzbiorach potrzebnych do wyznaczenia kwartyli. W związku z tym pierwszy podzbiór to: 1, 2, 3, 4, a drugi podzbiór to: 4, 5, 6, 7. Kwartyle obliczamy jako średnie pomiędzy dwoma elementami środkowymi i wynoszą odpowiednio Q1=2,5 oraz Q3=5,5.
Metoda trzecia:
Mediana wynosi 4. Liczba elementów w naszej populacji wynosi 7. Możemy to przedstawić za pomocą równania: 7=4*1+3. Korzystamy więc z drugiego podpunktu trzeciej metody:
Q1=0,75*x(1+1)+0,25*x(1+2).
Q1=0,75*2+0,25*3=2,25
Q3= 0,25*x(3+2)+0,75*x(3+3)
Q3=1,25+4,5=5,75
Podsumowując: dla parzystej liczby obserwacji mamy identyczne wyniki niezależnie od przyjętej metody. Dla nieparzystej liczby obserwacji wyniki różnią się w zależności od przyjętej metody obliczania poszczególnych kwartyli.
Rozstęp kwartylny i odchylenie ćwiartkowe
Jak już mamy obliczone wartości dwóch kwartyli, to możemy je od siebie odjąć (od górnego kwartyla dolny kwartyl) i w ten sposób otrzymujemy wartość, która w statystyce jest nazywana rozstępem kwartylnym albo ćwiartkowym. Rozstęp ten zapisuje się zwykle za pomocą skrótu IQR – pochodzi on od angielskiej nazwy interquartile range. Jest to miara, która sporo mówi o populacji, gdyż w tych granicach mieści się 50% (czyli dokładnie połowa) badanych obiektów. Im większy rozstęp kwartylny, tym bardziej zróżnicowana jest cecha statystyczna. Połowę rozstępu kwartylnego przyjęło się nazywać odchyleniem ćwiartkowym.
Uwagi końcowe
Wiele osób się myli i nie rozróżnia kwantyli od kwartyli. Mam nadzieję, że zorienowaliście się podczas lektury tego tekstu, że kwartyl to po prostu jedna z odmian kwantyla (ta, która dzieli populację na cztery części).
Przypominam, że mediany i kwartyle liczymy w szeregu uporządkowanym. Czyli trzeba sobie posortować wszystkie obserwacje od najmniejszej do największej.
A ponieważ dzisiejszy tekst wyszedł już niespodziewanie długi, to konkretne przykłady wykorzystania kwantyli przedstawię w kolejnym artykule. Planuję opisać między innymi tablice rozkładów i siatki centylowe. Zapraszam do czytania!
Droga Czytelniczko! Drogi Czytelniku!
Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.
Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.
A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.
Pozdrawiam Cię serdecznie i życzę miłego dnia!
Krystyna Piątkowska