Czy można być minimalistą w statystyce? Do czego można wykorzystać skrzyneczkę? Czy pudełko może mieć wąsy? Jak łatwo porównywać mediany? I czy my naprawdę musimy rysować?
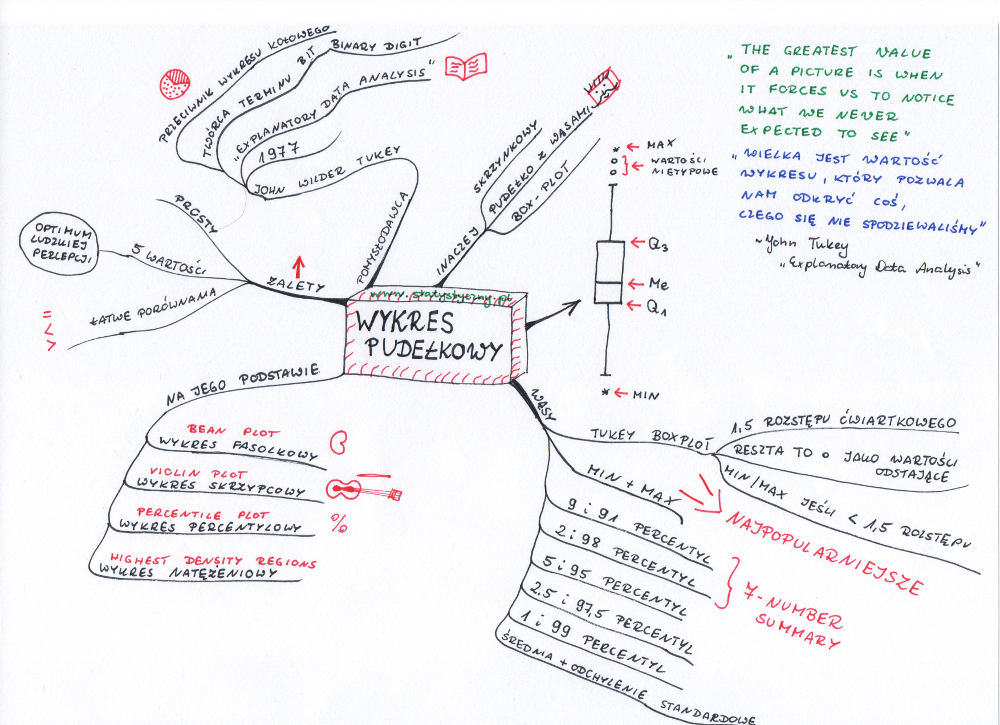
Dzisiaj znów zaproponuję małe ćwiczenia rysunkowe. Tym razem wykres pudełkowy z pięknymi wąsami. Wykres ten został zaproponowany w 1977 roku przez Johna Tukeya w książce „Explanatory Data Analysis”. W tej właśnie książce Tukey napisał, że „Wielka jest wartość wykresu, który pozwala nam odkryć coś, czego się nie spodziewaliśmy” (ang. „The gratest value of a picture is when it forces us to notice what we never expected to see”). Pokazywałam już we wpisie o histogramie, jak graficzne przedstawienie danych wspomaga nas w analizie i pomaga zauważyć fakty, których nie widać wyłącznie na podstawie obliczonych wskaźników. Dzisiaj chcę pokazać prosty wykres, który jest bardzo często zaniedbywany i niedoceniany, a w ciekawy sposób prezentuje miary pozycyjne (medianę, kwartyle, minimum i maksimum).
Wykres pudełkowy (zwany inaczej skrzynkowym, wykresem „pudełko z wąsami” albo z angielskiego box-plot), to wykres, który przedstawia tylko 5 informacji – jakby stworzony dla osób o minimalistycznym podejściu do życia. Bo mimo tak niewielu potrzebnych informacji, potrafi bardzo dużo przekazać. Musimy tylko znać dokładną wartość mediany, pierwszego i trzeciego kwartyla oraz minimum i maksimum – w efekcie możemy zaobserwować poziom rozproszenia populacji, sprawdzimy czy jest symetryczna, zobaczymy jak bardzo oddalone od mediany są wartości minimalne i maksymalne.
Jak narysować wykres pudełkowy?
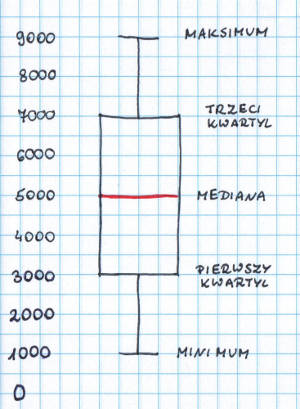
Gotowi do rysowania? Zacznijmy od przykładu, który już przerabialiśmy. Pamiętacie firmę „Wielka Niewiadoma”? To ta, w której mamy 10 pracowników, z których każdy zarabia inną kwotę (od 1000 zł do 9000 zł). Obliczaliśmy już dla niej medianę (5000 zł), obliczaliśmy kwartyle (3000 zł i 7000 zł). Znamy wartość minimalną (1000 zł) i maksymalną (9000 zł). W związku z tym nie ma problemu, żebyśmy od ręki narysowali wykres pudełkowy. Zaczynamy od pudełka. Pudełko to prostokąt, którego wartości wyznaczają poszczególne kwartyle. W naszym przypadku na osi zaznaczamy kreski na poziomie 3000 zł i 7000 zł. Łączymy je ze sobą, tworząc prostokąt (w klasycznym przypadku wykresu pudełkowego – szerokość prostokąta nie ma żadnego znaczenia. Na poziomie mediany zaznaczamy grubszą (lub kolorową – w naszym przypadku czerwoną) kreskę. Teraz pora na wąsy. Krótsze kreski zaznaczamy na poziomie 1000 zł oraz 9000 zł. Łączymy je z naszym pudełkiem linią prostopadłą i wykres gotowy.
Wykres ten możemy również stworzyć w R (korzystając z funkcji „boxplot”):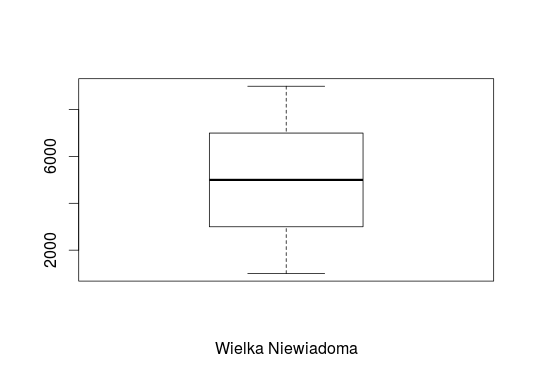
I można by było powiedzieć, że wszystko jasne i proste, gdyby nie fakt, że wąsy w wykresie pudełkowym rysowane są przez statystyków na różne sposoby. Warto o tym wiedzieć, żeby nie dać się zmylić nietypowemu wykresowi. Zawsze należy czytać, co oznaczają wartości wąsów. Opisany przed chwilą sposób jest najprostszy – opiera się po prostu na wartości minimalnej i maksymalnej.
Drugim bardzo popularnym wykresem jest tzw. „Tukey boxplot”, w którym wartości wąsów są wyznaczane przez półtora wartości rozstępu kwartylnego (ale tylko pod warunkiem, że minimum i maksimum są większe od tych wartości – w przeciwnym wypadku kończymy również na wartościach minimalnych i maksymalnych). Wszystkie wartości wykraczające poza wspomniany rozstęp kwartylny są zaznaczane kropką (albo gwiazdką albo jeszcze innym symbolem, a jak komuś chce się bawić, to zaznacza kropeczki dla wartości nietypowych, a gwiazdki zostawia dla minimum i maksimum). Uffff… znowu zabrzmiało skomplikowanie. Żeby jednak wszystko było jasne, wróćmy do naszego przykładu. W przypadku naszego wykresu rozstęp kwartylny to 4000 zł (7000 zł – 3000 zł). Gdybyśmy chcieli zaznaczyć wąsy na poziomie 1,5*IQR, to wyszłoby nam -3000 zł (3000 zł – 1,5*4000 zł) oraz 13000 zł (7000 zł + 1,5*4000 zł). Ponieważ minimum jest wyższe od wartości -3000 zł (1000 zł > -3000 zł), a maksimum jest niższe od wartości 13000 zł (9000 zł < 13000 zł), to nic się nie zmienia w naszym wykresie – wąsy pozostają na poziomie minimum i maksimum (czyli 1000 zł oraz 9000 zł).
Oprócz wspomnianych powyżej sposobów, używa się czasami wartości różnych percentyli (np. 9 i 91 percentyl, 2 i 98 percentyl, 5 i 95 percentyl, 2,5 i 97,5 percentyl, 1 i 99 percentyl), a także dostosowuje się wykres pudełkowy do miar klasycznych, używając średniej arytmetycznej i odchylenia standardowego zamiast mediany i kwartyli. Są to jednak sytuacje dużo rzadziej spotykane, w związku z czym tylko o nich wspominam, nie będziemy rysować wykresu dla każdego możliwego przypadku.
przykład wynagrodzeń
Spójrzmy lepiej na zalety wykresów pudełkowych. Bo oprócz tego, że rysuje się je naprawdę łatwo, to dają również duże możliwości porównawcze. Przypomnijmy sobie nasze 4 firmy, które analizujemy pod względem wynagrodzeń:
- „Wszystkim Równo” – zatrudnia 10 pracowników, z których każdy dostaje co miesiąc 5000 zł.
- „Szefo Górą” – zatrudnia panią sprzątaczkę, która na umowę zlecenie otrzymuje 500 zł, do tego 8 szeregowych pracowników z pensją 1500 zł i kierownika, który co miesiąc na konto przyjmuje 37500 zł.
- „Byle do Awansu” – mamy tu również 10 pracowników – pięciu pracuje poniżej roku i otrzymują 3000 zł, druga piątka ma już dłuższy staż i dzięki temu doczekała się pensji po 7000 zł.
- „Wielka Niewiadoma” – dziesięciu pracowników, każdy z inną pensją, od 1000 do 9000 zł.
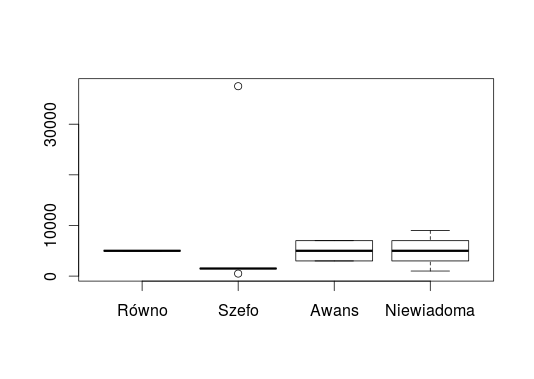
Poniżej przedstawiam wykres (przygotowany za pomocą R), na którym pokazane są 4 wykresy pudełkowe, po jednym dla każdej firmy. Wykresy te przedstawiają wykres pudełkowy Tukeya, czyli wąsy są na poziomie półtora rozstępu kwartylnego. Przypatrzmy się wszystkim po kolei. W firmie „Wszystkim Równo” cały wykres sprowadza się do jednej kreski, a to dlatego, że minimum, maksimum, mediana i kwartyle mają dokładnie taką samą wartość.
W przypadku firmy „Szefo Górą” pudełko i wąsy to też jedna kreska, ale mamy tu do czynienia z dwoma wartościami odstającymi – maksimum i minimum wykraczają poza wartość półtora rozstępu kwartylnego, w związku z czym zaznaczone są za pomocą kółeczek.
Firma „Byle Do Awansu” cechuje się niewielkim zróżnicowaniem wynagrodzeń. Pudełko przedstawia pierwszy i trzeci kwartyl (w wysokości 3000 zł oraz 7000 zł), medianę na poziomie 5000 zł oraz maksimum i minimum w wysokości odpowiadającej kwartylom (w efekcie wąsy nie występują).
Przykład firmy „Wielka Niewiadoma” pokazywaliśmy na samym początku tekstu, ale warto zauważyć, że jest to jedyna firma, której wykres posiada wąsy, a nie tylko pudełko (co świadczy o zróżnicowaniu wynagrodzeń). Samo pudełko wygląda identycznie jak w przypadku firmy „Byle do Awansu”, różnice widać przy obserwacji minimum i maksimum. Widać również, że wynagrodzenia odchylają się od mediany bardzo symetrycznie, nie ma również żadnych wartości nietypowych, odstających, które wykraczałyby poza poziom półtora rozstępu kwartylnego.
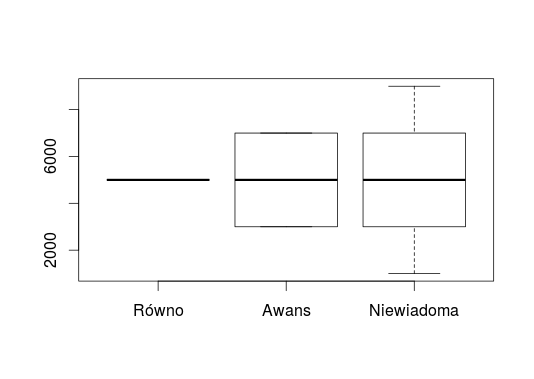
Ponieważ wynagrodzenie szefia w firmie „Szefo Górą” mocno różni się od pensji wszystkich innych pracowników ze wszystkich czterech firm, to przygotowałam też zestawienie, na którym są wykresy pudełkowe pozostałych trzech firm. Myślę, że różnice między nimi prezentują się na tym zestawieniu bardziej przejrzyście.
przykład ocen szkolnych
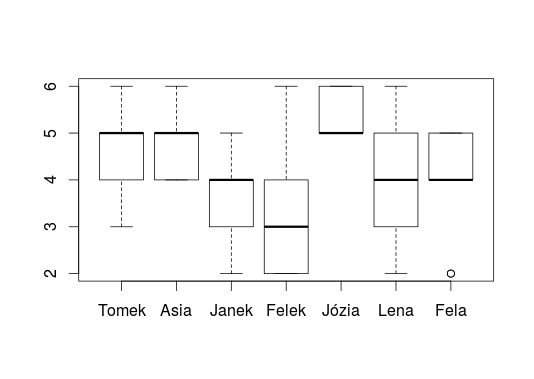
I jeszcze przykład porównawczy dla ocen szkolnych. Jesteśmy przyzwyczajeni, że zawsze liczy się tylko średnią arytmetyczną. A zobaczcie, jak ciekawie wygląda wykres porównawczy dla 7 uczniów:
Czy nie uważacie, że daje bardzo duże możliwości interpretacji ocen każdego ucznia?
Porównajmy powyższy wykres z informacją wyłącznie o średniej arytmetycznej (która jest często jedyną wartością interesującą nauczycieli, wychowawców czy rodziców):
| Tomek | Asia | Janek | Felek | Józia | Lena | Fela |
| 4.6 | 4.8 | 3.6 | 3.2 | 5.3 | 4 | 4 |
Moim zdaniem dużo więcej wniosków można wynieść poprzez analizę naszych wykresów pudełkowych. Zgadzacie się ze mną?
A na koniec ciekawostka specjalnie dla informatyków: czy wiecie, że Tukey jest twórcą nie tylko wykresu pudełkowego, ale również terminu „bit” (skrót od słów „binary digit”)?
Droga Czytelniczko! Drogi Czytelniku!
Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.
Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.
A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.
Pozdrawiam Cię serdecznie i życzę miłego dnia!
Krystyna Piątkowska