Statystyka nie jest bardzo trudna. Ale jak każda dziedzina wiedzy wymaga, żeby się z nią zaprzyjaźnić i dobrze zrozumieć. I jak każda dziedzina wiedzy ma swoje pułapki, które bardziej doświadczone osoby widzą na pierwszy rzut oka, a początkujący łatwo mogą w nie wpaść. Dzisiaj przedstawiam kilka podpowiedzi, na co warto zwrócić uwagę podczas swojej przygody ze statystyką. Co trzeba zrobić, żeby nie wpaść w pułapki statystyczne?
1. Czym jest tak naprawdę współczynnik korelacji Pearsona?
Korelacja to inaczej współzależność, która występuje pomiędzy dwoma zjawiskami. W statystyce poziom zależności liniowej między dwoma zmiennymi losowymi mierzy się za pomocą współczynnika korelacji liniowej Pearsona. Jego wartość zawsze mieści się w przedziale od -1 do 1. Im bliżej 0, tym mniejsza jest korelacja. Im bliżej 1 (lub -1), tym większa korelacja pomiędzy badanymi zmiennymi (dodatnia lub ujemna).
Pułapka tkwiąca we współczynniku korelacji Pearsona polega na tym, że bardzo często współzależność jest mylona ze związkiem przyczynowo-skutkowym. W statystyce mówiąc o korelacji, opisujemy siłę oraz kierunek zależności pomiędzy zmiennymi. Jeśli chcemy analizować związek przyczynowo-skutkowy, to zmieniając jedną zmienną, oczekujemy równocześnie zmiany drugiej zmiennej – zależnej. Ale żeby przekonać się, że istnieje taki związek przyczynowo-skutkowy, to musimy przeprowadzić nie tylko obserwację, ale eksperyment. Potrzebujemy grupę obserwowaną, grupę kontrolną, musimy starannie zaprojektować całe badanie. Dopiero, kiedy uzyskamy odpowiednie wyniki, możemy mówić o tym, że z pewnym prawdopodobieństwem jedna zmienna wpływa na drugą. A jeśli chodzi o korelację… zapamiętajmy jedno słynne angielskie zdanie: „Correlation does not imply causation”. Warto mieć je w głowie, kiedy na podstawie współczynnika korelacji Pearsona chcemy wyciągnąć zbyt daleko idące wnioski. A tym bardziej, kiedy ktoś próbuje nas do czegoś przekonać, opierając się na niepotwierdzonych eksperymentami obserwacjach.

Więcej w tekstach:
- Współczynnik korelacji Pearsona. O piratach, globalnym ociepleniu i Potworze Spaghetti
- Współczynnik korelacji Pearsona w przykładach
2. Uwaga na dowody anegdotyczne
„To musi być prawda, bo u mnie działa.”
„Moje dziecko chorowało i jak tylko dostało tabletki homeopatyczne, to zaraz było zdrowe.”
„Na problemy z bezsennością najlepszy jest kubek ciepłego mleka. Na pewno ci pomoże.”
„Zobacz, jaka brzydka pogoda za oknem, globalne ocieplenie to jakaś bzdura.”
Jakże często słyszymy tego typu zdania. Opinie wyrażane przez osoby, które są przekonane o swojej racji. I swoje przypuszczenia, pojedyncze przypadki (zupełnie nieprzebadane) uogólniają na wszystkich. Są to przykłady dowodów anegdotycznych. O dowodzie anegdotycznym mówimy w dwóch przypadkach. Po pierwsze w sytuacji, kiedy mamy do czynienia z informacją fałszywą, która jest przedstawiana jako prawdziwa. Po drugie wtedy, kiedy mamy do czynienia z informacją prawdziwą, ale niezweryfikowaną. Niebezpieczeństwem dowodu anegdotycznego jest fakt, że osoba przedstawiająca go innym jest w 100% pewna swojej racji. Skoro u niej zadziałało, to w dobrej wierze przekazuje informację kolejnym osobom, z pełnym przekonaniem, że tak właśnie jest. Trzeba bardzo uważać, żeby nie tylko nie nabrać się na dowody anegdotyczne, ale również nie stać się ich źródłem.
Więcej: Dowód anegdotyczny. Czy jedzenie marchewki przedłuża życie?
3. Paradoks Simpsona (czyli uwaga na procenty)
W 1973 roku Uniwersytet Kalifornijski w Berkley został oskarżony o dyskryminację kobiet. Analiza wykazała, że przyjęli na studia 44% starających się mężczyzn i tylko 35% kobiet. Taka dyskryminacja, to poważny zarzut więc temat został szczegółowo przeanalizowany. Poszczególne wydziały zaprezentowały swoje własne dane dotyczące rekrutacji. I okazało się, że w większości przypadków widać było więcej przyjęć wśród przedstawicielek płci pięknej? Jak to możliwe? Wszystko dlatego, że procent procentowi jest nierówny. Jeśli mamy do czynienia z 20% ze 100 i 20% z 1000, to raz będzie to 20, a raz 200. Procent natomiast za każdym razem taki sam. Jeśli więc panie zdawały na bardziej oblegane kierunki, to wyniki rekrutacji na całej uczelni mogą wyglądać zupełnie inaczej niż wyniki na poziomie wydziałów.
Inny znany przykład paradoksu Simpsona pochodzi z dziedziny badań medycznych. Badano skuteczność dwóch metod leczenia kamicy nerkowej: operacji chirurgicznych oraz PCNL. W przypadku małych kamieni operacje chirurgiczne kończyły się sukcesem w 93% przypadków (81/87), natomiast PCNL w 87% przypadków (234/270). Jeśli chodzi o duże kamienie nerkowe, to operacje chirurgiczne zakończone sukcesem stanowiły 73% przypadków (192/263), a PCNL 69% (55/80). Jeśli podsumujemy wszystkie dane, to zauważymy, że sumarycznie udane operacje chirurgiczne stanowią 78% (273/350), a PCNL 83% (289/350). Jak to możliwe, że sumarycznie udane operacje chirurgiczne wydają się być miej skuteczne od PCNL, skoro i dla małych i dla dużych kamieni cechowały się większą skutecznością? Tutaj kwestia leży w trudności poszczególnych sposobów leczenia. Operacje chirurgiczne stosuje się wtedy, kiedy mamy do czynienia z bardziej wymagającymi przypadkami medycznymi i wyleczenie pacjenta jest trudniejsze.
Dlaczego poznanie Paradoksu Simpsona jest tak ważne? Bo w zależności od tego, które wyniki nam zostaną zaprezentowane – możemy być łatwo przekonywani, że jedna z metod jest bardziej skuteczna od drugiej.
Więcej: Paradoks Simpsona. O dyskryminacji kobiet, kamicy nerkowej i bezrobociu.
4. Kwartet Anscombe’a
Pułapki statystyczne – ciąg dalszy. Kwartet Anscombe’a przekonuje nas, jak bardzo ważna jest wizualizacja danych. Lata 70-te XX wieku to były czasy, kiedy wszyscy skupiali się coraz bardziej na analizie danych. Pojawiały się coraz większe możliwości obliczeniowe, coraz łatwiej było wyliczyć przeróżne charakterystyki statystyczne. I właśnie wtedy Anscombe napisał pracę „Graphs in Statistical Analysis”, w której podkreśla, że u podstaw wszystkiego leży zrozumienie zjawiska, zrozumienie istoty danych, które analizujemy. Dopomóc w tym może graficzne przedstawienie zmiennych. I zaproponował cztery zestawy danych. Co je łączy? Taka sama: średnia arytmetyczna zmiennej x, wariancja zmiennej x, średnia arytmetyczna zmiennej y, wariancja zmiennej y, współczynnik korelacji pomiędzy zmiennymi, równanie regresji liniowej. Wszystkie cztery zestawy wydają się być bardzo podobne – skoro łączy je tyle statystyk. Tymczasem patrząc na wykresy widzimy zdecydowanie różniące się między sobą zależności pomiędzy zmienną x i y.
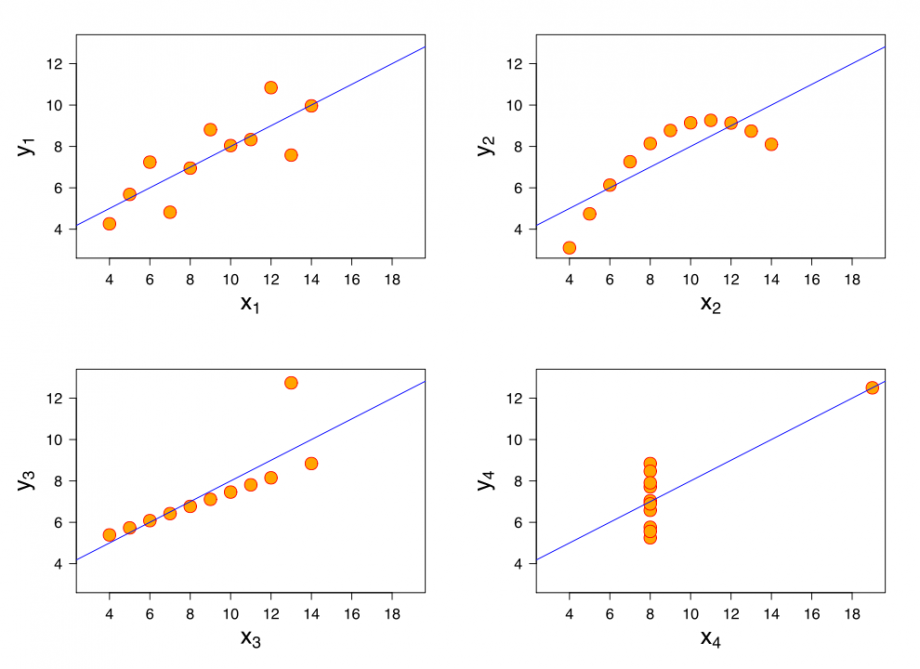
Anscombe przypomina, że badane zjawiska statystyczne to nie tylko zestaw liczb. To nie tylko obliczone statystyki. To są zjawiska, które warto zobaczyć i zrozumieć, zanim zaczniemy je analizować.
A jak już jesteśmy przy temacie kwartetu Anscombe’a, to przypominam jeszcze o Datasaurusie (Danozaurze?). Jest to jeszcze ciekawszy przykład na wizualizację danych. Mój ulubiony statystyczny temat. I jeśli interesują Was nie tylko pułapki statystyczne, ale również statystyczne ciekawostki, to tę szczególnie polecam. Czytajcie o Datasaurusie!
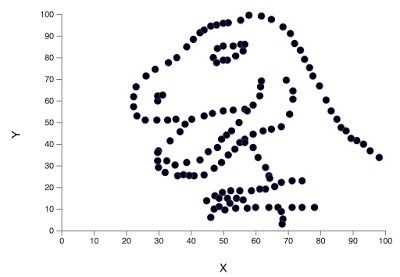
Więcej: Kwartet Anscombe’a, Datasaurus – czyli po co w ogóle rysować?
5. Efekt Hawthorne
Efekt Hawthorne to bohater jednego z moich ostatnich wpisów na blogu, ale przypomnę o nim też tutaj, bo jest to dość istotny temat. Mówi on o tym, że ludzie zmieniają swoje zachowanie albo swoje działania, kiedy mają świadomość, że są obserwowani albo poddawani badaniu. Czyli jeśli wiem, że ktoś mnie obserwuje, to zachowuję się inaczej niż gdybym była w tym momencie sama. Jeśli mam wypełnić ankietę, to będę przedstawiać siebie w jak najlepszym świetle. I nawet jeśli będę zapisywać swoje własne osiągnięcia, to postaram się, żebym miała do zapisu to, co najlepsze.
A jaka w tym pułapka?
Kiedy przeprowadzamy ankietę albo przeprowadzamy eksperyment i obserwujemy ludzi, to musimy za każdym razem brać pod uwagę, że wyniki naszych badań najprawdopodobniej są zniekształcone właśnie przez efekt Hawthorne. Nie wiadomo do jakiego stopnia, nie wiadomo dokładnie w jaki sposób. Niemniej jednak warto być na to przygotowanym i przynajmniej mieć świadomość takiego zniekształcenia.
Więcej: Efekt Hawthorne – badanie zachowań ludzkich bywa naprawdę trudne
Czy to już wszystkie pułapki statystyczne? Zdecydowanie nie!
6. Średnia średniej nierówna
Kiedy mówimy o średniej, to od razu do głowy przychodzi nam średnia arytmetyczna. To do niej jesteśmy przyzwyczajeni i to jej najczęściej się używa. Począwszy od świadectwa szkolnego, towarzyszy nam przez całe życie. Ale nie jest to jedyna średnia. Średnia trymowana, średnia harmoniczna, średnia geometryczna czy chronologiczna – o nich pisałam już na moim blogu. A jeszcze można trafić na takie pojęcia jak średnia ważona, średnia kwadratowa, średnia potęgowa, winsorowska czy logarytmiczna… Średnich tyle, że hoho. I kiedy której z nich używać? Czy możemy zawsze arytmetyczną i tyle?
No nie do końca. Obliczając średnią prędkość należy skorzystać ze średniej harmonicznej. Szukając materiału na powłokę antyrefleksyjną w okularach, warto pamiętać o średniej geometrycznej. W gąszczu średnich należy się zorientować, kiedy która jest najbardziej przydatna, żeby nie wpaść w pułapkę i nie stwierdzić, że jeśli na trasie o długości 10 km pierwsze 5 km przebiegliśmy w tempie 10 km/h, a kolejne 5 km przebiegliśmy w tempie 5 km/h, to średnia prędkość na naszej trasie wynosiła 7.5 km/h. W rzeczywistości średnia prędkość na naszej trasie to 6 i 2/3 km/h. A całą trasę zrobiliśmy w 90 minut. Gdyby średnia prędkość wynosiła 7.5 km na godzinę, to potrzebowalibyśmy tylko 80 minut na przebiegnięcie całej trasy.
Tak więc nie dajmy się wpuścić również w pułapkę ze średnimi. Bo jak już napisałam – średnia średniej nierówna.
Więcej:
- średnio na jeża, czyli średnia arytmetyczna
- średni kurs NBP i słów kilka o średniej trymowanej
- dlaczego fizyk i rowerzysta powinni znać średnią harmoniczną
- O zaludnieniu, napełnianiu basenu i średniej harmonicznej w trapezie
- Co łączy soczewki antyrefleksyjne i współczynniki inflacji? O średniej geometrycznej.
- Co to jest średnia chronologiczna?
7. Pułapki statystyczne na wykresach
Kiedy pisałam o różnych wykresach statystycznych pokazywałam, że są wśród nich takie, które zniekształcają to, co chcemy przedstawić. Pamiętacie być może wykres tortowy?
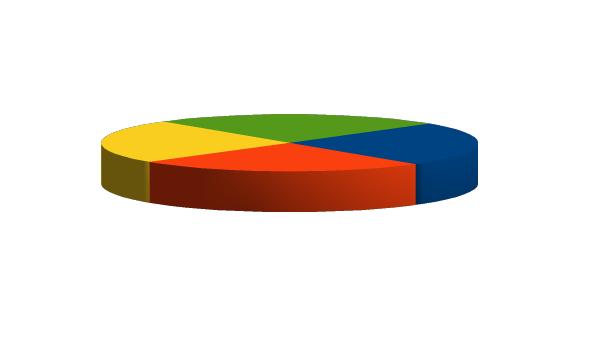
Tak, niby żółtego, zielonego, niebieskiego i czerwonego jest na nim tyle samo, ale zdecydowanie na to nie wygląda, prawda? Jak jeszcze trochę byśmy tym wykresem pokręcili w przestrzeni, to możemy optycznie każdy z kolorów tak podkreślić, żeby zdominował pozostałe i dał złudzenie, że stanowi większość.
Ciekawym pomysłem były też pawie oczka – wykres polityczny sprzed 9 lat, który zdecydowanie manipulował tym, co chciał nam pokazać. Intuicyjnie patrzymy na pola powierzchni, a nie długości średnic, prawda? A autor wykresu właśnie na średnicach poszczególnych kółek oparł swoje dane. Do tego nie wiadomo, czy wyborcy PIS i Kukiz’15 zawierają się w tych, którzy na nich nie głosowali (skoro są w środku dużego kółka), czy jeszcze inne tajemnicze rzeczy miały tam miejsce…

Przykłady można by było mnożyć – często można natrafić na zestawienia najbardziej absurdalnych wykresów prezentujących jakieś dane. Ja tu pozostawię tylko dwa powyższe obrazki, niech dadzą do myślenia. A Wy zawsze przyglądajcie się skali, opisowi, liczbom i innym detalom, które mogą pokazać, że autor wykresu nie do końca poradził sobie z prostą wizualizacją danych.
Więcej:
- Pełen kontrowersji – wykres kołowy
- Torcik na dokładkę? Wykres kołowy w przestrzeni
- pawie-oczka-na-choinkę
8. Pozytywny wynik testu nie zawsze oznacza, że coś się wydarzyło
Testy ciążowe, covidowe, grypowe. Badania mammograficzne. Testy na boreliozę. Przeróżne badania krwi. Jakoś tak nauczyliśmy się wierzyć w to, że to co nam pokaże wynik, jest zawsze prawdziwe. A większość z tych testów czy badań ma jakąś swoją czułość i swoistość. Czyli to nie jest tak, że 100 procent chorych osób zostanie zakwalifikowanych jako chorzy i 100 procent zdrowych jako zdrowe osoby. Za każdym razem borykamy się z ryzykiem przypadków FP i FN (czyli fałszywie pozytywnych i fałszywie negatywnych). A najgorsze jest to, że jeśli zmniejszamy liczbę fałszywie pozytywnych przypadków, to chcąc nie chcąc automatycznie zwiększamy ryzyko fałszywie negatywnych. I odwrotnie.
Temat jest bardzo obszerny, ale najważniejsze co z tego wynika, że jeśli z jakiegoś badania wyjdzie Wam pozytywny wynik, a Wy czujecie się zupełnie zdrowi, to warto uzupełnić diagnostykę. Być może jest to fałszywie pozytywny wynik i dodatkowe badania, konsultacje, obserwacje doprowadzą do wykluczenia choroby. Jeśli macie natomiast wyraźne objawy chorobowe (i nie tylko), a wynik testu wyszedł negatywny, to warto dalej obserwować swój organizm, uzupełnić badania, powtórzyć, skonsultować z kimś wiarygodnym. Zawsze jest możliwość, ze to fałszywie pozytywny wynik testu.
Więcej:
- Czułość a swoistość – dlaczego musimy się tym martwić?
- Współczynnik Youdena, jak połączyć czułość i swoistość i znaleźć punkt odcięcia
Pułapki statystyczne – podsumowanie
Pułapki statystyczne czają się dookoła i warto wiedzieć, że nie wszystko wygląda zawsze tak, jak na pierwszy rzut oka by się wydawało. I jeśli mamy jakiekolwiek wątpliwości to warto rzucić tym okiem po raz drugi. A najlepiej dokształcić się na tyle, żeby żadne pułapki nie były nam straszne.
A może ktoś z Was ma jeszcze jakieś spostrzeżenia w tym temacie? Może daliście się nabrać na coś, na co absolutnie nie powinniście nigdy dać się nabrać?
Tekst „pułapki statystyczne” to taka moja próba podsumowania kilku ważnych tematów, które opisywałam już wcześniej na blogu. Bardzo staram się zawsze podkreślić, jak do takich pułapek podchodzić. Mam nadzieję, że mi się udało. Co o tym sądzicie? Napiszcie w komentarzu. Możecie też odezwać się na facebooku albo napisać do mnie maila.
Jeśli uważacie, że to co piszę jest wartościowe, to od niedawna możecie się zrzucić na symboliczną „kawkę”. To dodaje skrzydeł i motywuje do dalszego pisania.
Ja natomiast zapraszam Was na facebooka, sugeruję skorzystanie ze spisu treści i wybranie sobie czegoś ciekawego do przeczytania. Jakie są Wasze ulubione artykuły? Czy tekst „pułapki statystyczne” do nich dołączy?
Pozdrawiam ciepło i serdecznie!
Krystyna Piątkowska