Czy słyszeliście kiedyś o średnim kursie NBP? A czy wiecie jak się go liczy?

Intuicyjnie, powinna to być średnia arytmetyczna kursów zebranych ze wszystkich kantorów w całym naszym kraju. Ale czy tak jest rzeczywiście? Jak nasz Narodowy Bank Polski w rzeczywistości liczy kursy podawane w swoich tabelach?

Jak można domyślić się, codzienne zbieranie wszelkich wartości kursów jest nieopłacalne. Poza tym kursy zmieniają się z godziny na godzinę. Inne będą w Warszawie, inne w Poznaniu, a jeszcze inne w Ustrzykach Dolnych. Każdy kantor, każdy bank może w każdej chwili zmienić kurs wymiany i po 5 minutach sprzedawać waluty w innej cenie niż jeszcze chwilę wcześniej. Skąd się więc biorą średnie kursy publikowane codziennie przez NBP?

NBP skupia się przede wszystkim na kursie euro i dolara amerykańskiego (EUR i USD). Ma swoją listę 10 banków, do których zwraca się pomiędzy godziną 10:55 a 11:00 z zapytaniem o kurs sprzedaży i zakupu tych walut. Następnie sumuje kurs sprzedaży i zakupu danej waluty w każdym banku i dzieląc sumę przez 2, oblicza znaną nam już średnią arytmetyczną. Żeby pozbyć się wartości skrajnych (wspominałam w poprzednim wpisie, że średnia artytmetyczna szczególnie ich nie lubi), z tych dziesięciu średnich NBP odrzuca dwie najwyższe i dwie najniższe. A z pozostałych sześciu znowu liczy średnią arytmetyczną. I ta oto średnia trafia codziennie do tabeli, z której korzystają… no właśnie… kto korzysta z tych średnich kursów NBP? Na pewno rzesza księgowych (dla których szczególnie istotne są kursy z ostatniego dnia roku, potrzebne do wyceny wszystkich walutowych składników majątku do bilansu), a poza tym?

No i co z pozostałymi kursami? Przecież na euro i dolarze tabele NBP się nie kończą.

Kursy walut, które znajdujemy w tabeli A (czyli można powiedzieć, że te bardziej popularne) są obliczane codziennie na podstawie wyliczonego kursu EUR (w złotych) oraz rynkowych kursów EUR do poszczególnych walut z godziny 11.00 (a rynkowe kursy brane są z serwisów informacyjnych Thomson Reuters, Bloomberg).

Kursy pozostałych walut (tabela B) są liczone raz na tydzień (w każdą środę) i również korzysta się z obliczonego kursu euro oraz rynkowych kursów z serwisów informacyjnych.

I tak oto, wykorzystując tylko samą wiedzę o średniej arytmetycznej, dowiedzieliśmy się, jak NBP liczy kursy walut. I myślę, że każdy z czytelników sam by sobie poradził z takimi obliczeniami 🙂

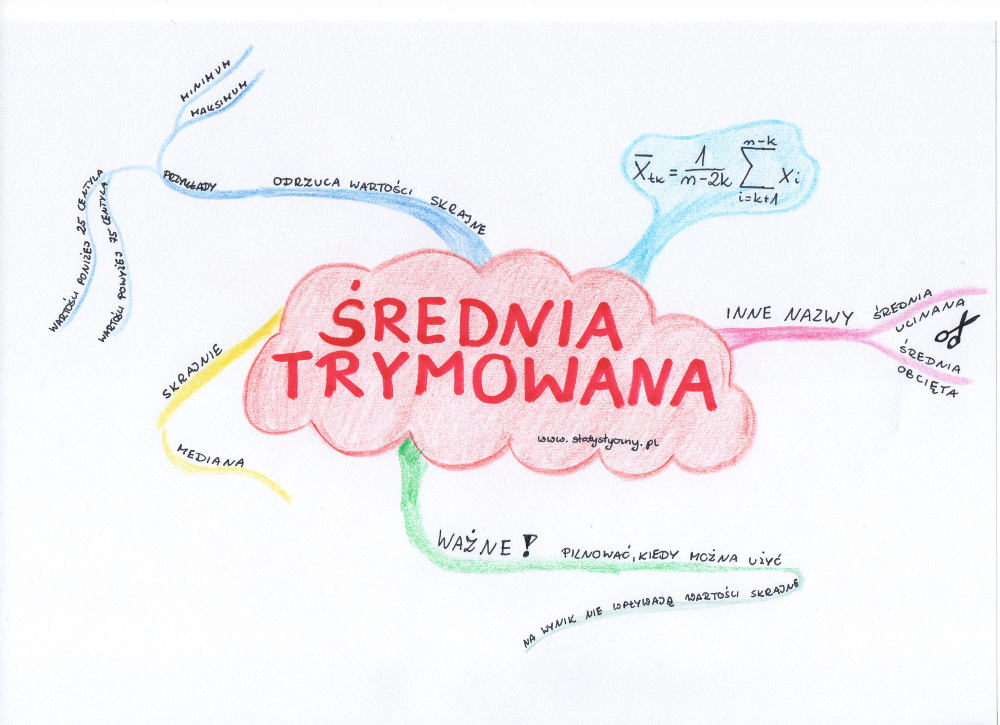
Średnia trymowana, ucinana, obcięta

Jeszcze jedna sprawa – już pod poprzednim wpisem o średniej arytmetycznej pojawiło się pytanie, czy średnia arytmetyczna liczona po odrzuceniu wartości skrajnych jest nadal średnią arytmetyczną. Uważam, że nadal można nazwać ją średnią arytmetyczną, tylko trzeba podkreślić, że jest ona liczona na podstawie innej populacji. W statystyce istnieją również nazwy specjalnie dla takiej średniej. Jest to średnia ucinana, średnia obcięta lub średnia trymowana.

Przy obliczaniu takiej średniej obserwacje porządkuje się od najmniejszej do największej, odrzuca się mały procent najbardziej ekstremalnych obserwacji na obu krańcach (wartości najmniejsze oraz największe), na ogół równej liczności, a następnie oblicza się średnią arytmetyczną z pozostałych obserwacji.

\(\overline{x}_{tk}= \frac{1}{n-2k}\sum_{i=k+1}^{n-k}x_{i}\)

 

Zwyke odrzuca się minimum i maksimum z próbki lub wartości poniżej 25 centyla i powyżej 75 centyla (czyli 1/4 najniższych i najwyższych obserwacji).

W przykładzie z NBP odrzucane są 2 wartości najniższe i dwie wartości najwyższe (k=2).

Średnia trymowana jest wykorzystywana w zawodach sportowych (np. skoki narciarskie), gdzie uwzględnia się oceny sędziów z pominięciem jednej najwyższej i najniższej (k=1).

Celem takiej modyfikacji średniej arytmetycznej jest pozbycie się wpływu wartości skrajnych na wynik. Trzeba jednak uważać. Nie zawsze średnia trymowana jest lepsza od średniej arytmetycznej. Wróćmy do przykładu z nasypywaniem mąki do kilogramowych torebek. Załóżmy, że maszyna się rozregulowała i co dziesiąta torebka dostaje dwa kilogramy mąki zamiast jednego. Jeśli postanowimy policzyć średnią obciętą i “obetniemy” po 10% najniższych i po 10% najwyższych wyników, to wszystkie nasze dwukilogramowe torebki nie zostaną uwzględnione. Pozostanie tylko błędne wrażenie, że wszystko jest w porządku.

przykład średniego wynagrodzenia

Możemy też wrócić do naszego przykładu z wynagrodzeniem pracowników:

1. „Wszystkim Równo” – zatrudnia 10 pracowników, z których każdy dostaje co miesiąc 5000 zł.
2. „Szefo Górą” – zatrudnia panią sprzątaczkę, która na umowę zlecenie otrzymuje 500 zł, do tego 8 szeregowych pracowników z pensją 1500 zł i kierownika, który co miesiąc na konto przyjmuje 37500 zł.
3. „Byle do Awansu” – mamy tu również 10 pracowników – pięciu pracuje poniżej roku i otrzymują 3000 zł, druga piątka ma już dłuższy staż i dzięki temu doczekała się pensji po 7000 zł.
4. „Wielka Niewiadoma” – dziesięciu pracowników, każdy z inną pensją, od 1000 do 9000 zł.

Licząc średnią trymowaną, która nie uwzględnia jednej najwyższej i jednej najniższej wartości (k=1), otrzymujemy kolejno następujące wyniki: 5000 zł, 1500 zł, 5000 zł oraz 5000 zł. Czyli tylko w przypadku sytuacji, kiedy zarobki szefa znacznie przewyższały wszystkie pozostałe, pominięcie wartości skrajnych wykazało jakikolwiek wpływ na obliczaną średnią. W innych firmach nadal otrzymywaliśmy wiadomość o średnim wynagrodzeniu równym 5000 zł.

wyjaśnienie wzoru

Dla laików matematycznych wyjaśnienie wzoru:

\(\overline{x}_{tk}= \frac{1}{n-2k}\sum_{i=k+1}^{n-k}x_{i}\)

 

Liczymy średnią trymowaną o parametrze k. Parametr k oznacza, ile najmniejszych i ile największych wartości chcemy odrzucić (jeśli odrzucamy jedną najbardziej ekstremalną, czyli minimum i maksimum, to k=1). Następnie sumujemy wszystkie wartości, które pozostaną nam po odrzuceniu skrajnych. Uzyskaną sumę dzielimy przez liczbę sumowanych wartości.

przykład obliczeń

Załóżmy, że nasz skoczek narciarski otrzymał od sędziów 5 not: 17.5, 18, 18.5, 19 i 20. Jaka będzie średnia nota zaliczona do jego wyniku?

Najpierw odrzucamy wartości skrajne – minimum i maksimum. Pozostaje nam: 18, 18.5 i 19. Sumujemy pozostałe wartości i otrzymujemy 55.5. Po podzieleniu przez 3 (tyle wartości sumowaliśmy) otrzymujemy 18.5 i to jest nasza średnia trymowana.

Gdybyśmy liczyli średnią arytmetyczną, to wyniosłaby ona 18.6.

---

Droga Czytelniczko! Drogi Czytelniku!

Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.

Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.

A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.

Pozdrawiam Cię serdecznie i życzę miłego dnia!

Krystyna Piątkowska