O różnych wykresach pisałam jakiś czas temu, ale wykres punktowy nie zasłużył wtedy na moją uwagę. Nieśmiało próbował się wtrącić w artykułach na temat korelacji, ale nadal nie czuje się usatysfakcjonowany. Postanowiłam więc naprawić moje zaniedbanie i tym razem cały tekst poświęcić właśnie temu wykresowi. Kochani Czytelnicy, przed Wami wykres punktowy!
Ucząc się o wykresie punktowym, mogliście słyszeć inne nazwy. Wykres rozproszenia, rozrzutu albo punktowy diagram korelacji. Z takimi nazwami ja spotkałam się w różnych miejscach (a może są jeszcze inne?). Po angielsku najczęściej używaną nazwą jest „scatter plot”, ale może też być kilka innych (na szczęście mają w nazwie zawsze scatter, więc łatwo skojarzyć, że wszystkie dotyczą tego samego wykresu): scatter diagram, scattergram, scatter graph albo scatter chart.
Kiedy rysujemy wykres punktowy? Najczęściej wtedy, kiedy mamy do czynienia z dwoma cechami i chcemy narysować zależność między nimi. Chcemy sprawdzić, czy występuje korelacja, jaki kierunek ma zależność, jaka jest siła relacji między zmiennymi i czy występują wartości nietypowe. Rysujemy wtedy dwie osie (tak jak na matematyce było z układem współrzędnych) i na jednej z nich oznaczamy jedną cechę statystyczną, a na drugiej drugą cechę. Następnie zaznaczamy dla wartości jednej cechy, jakie wartości przyjmuje druga cecha. Zabrzmiało bardzo skomplikowanie, prawda? Ale wcale takie nie jest – zaraz pokażę wszystko na przykładzie i powinno być już jasne.
Wykres punktowy – przykład zależności pomiędzy wagą i wzrostem
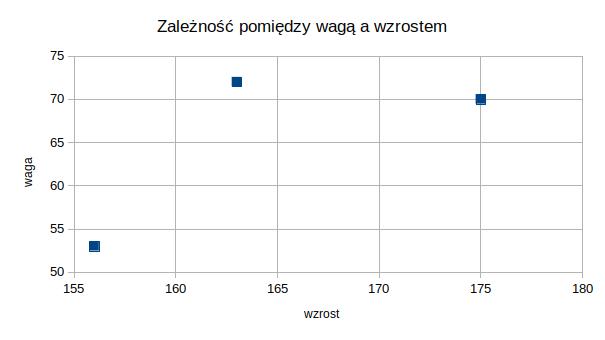
Mamy trzy panie: Anię, Olę i Emilkę. Ania mierzy 175 cm i waży 70 kg. Ola ma 156 cm i 53 kg. Dla Emilki mamy odpowiednio 163 zm i 72 kg. Spróbujmy przedstawić to na wykresie punktowym:
Na naszym wykresie na jednej osi mamy wzrost a na drugiej osi mamy wagę. Zaznaczone są trzy punkty – każdy z nich odpowiada jednej z analizowanych pań. Najniższa Ola to punkt 156 na osi wzrostu i 53 na osi wagi. Emilce odpowiada punkt 163 na osi wzrostu i 72 na osi wagi. Dla Ani mamy odpowiedno wartości 175 i 70.
Zazwyczaj do czynienia mamy z dużo większą liczbą jednostek statystycznych, które przedstawiamy na wykresie (w tym wypadku każda z pań to jednostka statystyczna, a analizujemy takie cechy tej jednostki jak wzrost i waga). Chciałam jednak pokazać na takim przykładzie, żeby każdy mógł sobie przypasować dane do konkretnej osoby i nie zgadywać, który punkcik co może oznaczać.
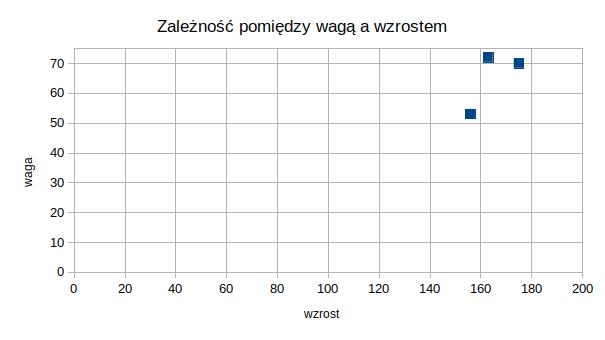
Warto również zwrócić uwagę na fakt, że punkt przecięcia naszych osi wcale nie musi być w 0. Na wykresie powyżej oś wzrostu zaczyna się od 155 cm, a oś wagi zaczyna się od 50 kg. Dzięki temu wykres jest bardziej czytelny. Poniżej zobaczmy wykres dla tych samych danych, ale gdzie miejsce przecięcia wyznacza 0:
Większość wykresu jest pusta, a istotne wartości pojawiają się gdzieś tam w kąciku.
Wykres punktowy – inne przykłady
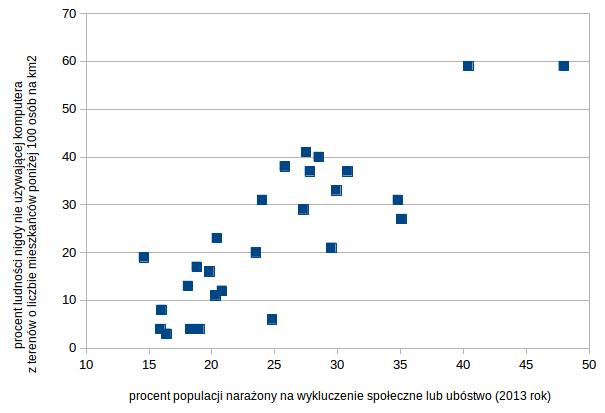
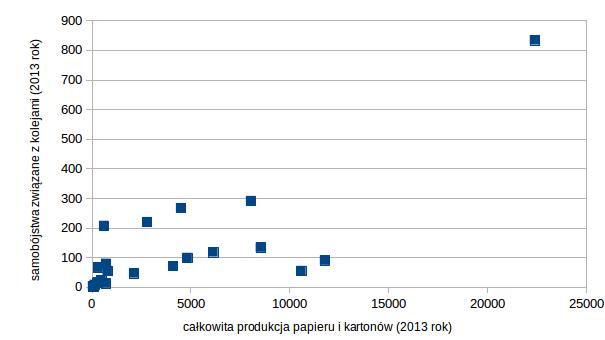
Pamiętacie jeszcze, że takie same wykresy przedstawiałam (bez wyjaśnienia jak je narysować), kiedy pisałam o współczynniku korelacji Pearsona? Bo właśnie wykres punktowy jest bardzo przydatny przy analizie korelacji. Pokazuje, z jaką zależnością mamy do czynienia i czy nie występują przypadki nietypowe (ang. outliers), które mogą zakłócić wartość współczynnika.
Przykład wykresu punktowego przedstawiającego pozytywną korelację między cechami:
Przykład wykresu punktowego przedstawiającego brak korelacji między cechami z jednym wyraźnym przypadkiem nietypowym, wpływającym na wartość współczynnika korelacji:
Co jeszcze można zrobić z wykresem punktowym?
Wykres punktowy czasem bywa kolorowy. Zaznaczając np. wagę i wzrost uczniów jednej klasy, można jeszcze podzielić dzieci ze względu na płeć i chłopców rysować jednym kolorem, a dziewczynki innym. Dzięki temu nie tylko zobaczymy relację między wagą i wzrostem, ale jeszcze możemy zaobserwować, czy relacja ta różni się w zależności od płci.
Można dodać trzeci wymiar i narysować wykres dla trzech zmiennych.
Można szukać na wykresie korelacji nieliniowych. Nie zawsze między dwoma danymi występuje korelacja liniowa. Wykres pozwala nam zobaczyć, czy mamy do czynienia z zupełnie inną zależnością i szukać odpowiedniego sposobu, który jak najlepiej opisze tę relację.
Macie jeszcze jakieś inne pomysły, do czego można wykorzystać wykres punktowy? Zapraszam do dzielenia się swoimi przykładami.
Zachęcam serdecznie do polubienia strony bloga statystycznego na facebooku. Umieszczam tam informacje o nowych wpisach i przypominam starsze artykuły. Każdy obserwator jest bardzo mile widziany.
Jeśli zainteresował Cię powyższy artykuł, to zapraszam do zapoznania się z pozostałymi tekstami prezentowanymi na blogu. Najlepiej skorzystać ze spisu treści.
Droga Czytelniczko! Drogi Czytelniku!
Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.
Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.
A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.
Pozdrawiam Cię serdecznie i życzę miłego dnia!
Krystyna Piątkowska