Hurrra! Wiemy już, co to jest średnia harmoniczna. W obliczeniach niezbyt przyjazna, w zrozumieniu jeszcze gorsza. Żeby więc ułatwić trochę przyjaźń z tą średnią, postanowiłam przedstawić jeszcze kilka przykładów. Przed Wami opowieść o napełnianiu basenu, obliczenia związane ze średnim zaludnieniem oraz na deser przykład wykorzystania średniej harmonicznej w geometrii. Zapraszam do lektury!
średnia harmoniczna – przykład basenu
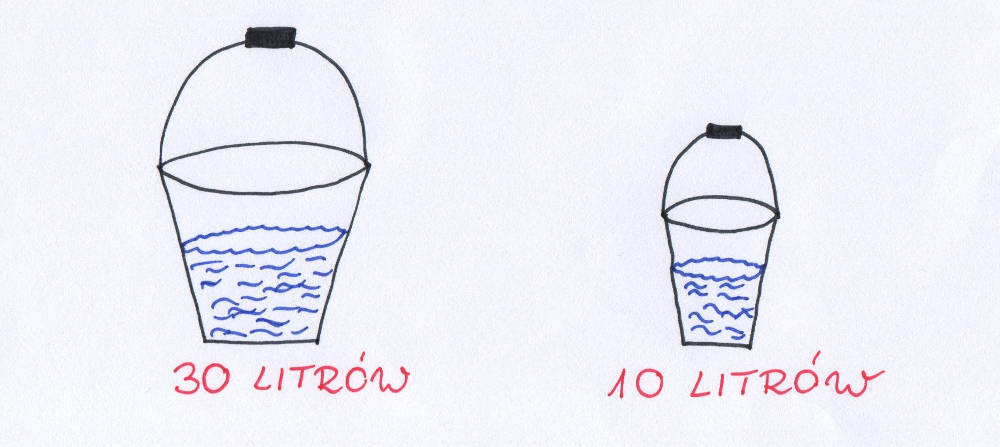
Zacznijmy od przykładu z basenem. Załóżmy, że mamy w ogródku basenik, do którego chcemy nalać 120 litrów wody. Wodę wymieniamy raz na tydzień. Ja noszę ją w wiaderku 10-litrowym i każda trasa pomiędzy domem a basenem zajmuje mi 10 minut. Cały basenik napełniam w czasie dwóch godzin (120 minut). Mąż mój jest zdecydowanie silniejszy i nosi wodę w 30-litrowym wiadrze. Trasa pomiędzy domem i basenem również zajmuje mu 10 minut. W związku z tym cały basenik napełnia w czasie 40 minut. Ile czasu potrzebujemy, żeby napełnić basenik wspólnie?
Najpierw obliczmy nasz średni czas napełniania basenu:
Jedna osoba pracująca w naszym średnim tempie potrzebuje do napełnienia basenu 60 minut. Dwie takie osoby zrobią to w 30 minut.
Czy to się zgadza? W ciągu każdych 10 minut wlejemy do basenu 40 litrów wody (30+10). Czyli po 30 minutach 120-litrowy basen będzie pełen.
Co by się stało, gdybyśmy próbowali użyć średniej arytmetycznej?
\(\overline{x}=\frac{40+120}{2}=\frac{160}{2}=80\)Gdybyśmy wyliczyli średnią arytmetyczną, to by wyszło, że jedna osoba pracująca w naszym średnim tempie potrzebuje 80 minut na napełnienie basenu wodą. W związku z czym dwie osoby potrzebują na to 40 minut. Ale skoro my w 10 minut przynosimy 40 litrów wody do basenu, to w 40 minut byśmy przynieśli 160 litów. Średnia arytmetyczna znów okazuje się być złym wyborem.
średnia harmoniczna – przykład średniego zaludnienia
Załóżmy, że mamy cztery gminy. W każej z tych gmin mieszka sto tysięcy osób. Każda ma natomiast zupełnie inną powierzchnię. Największa ma powierzchnię 100 km², potem kolejno 50 km², 25 km² oraz 20 km². Jaka jest średnia gęstość zaludnienia w tych gminach?
Przejdźmy do obliczeń. W pierwszej gminie średnie zaludnienie to 1 tysiąc osób/km², w drugiej – 2 tysiące osób/km², w trzeciej – 4 tysiące osób/km², natomiast w czwartej gminie mieszka średnio 5 tysięcy osób/km². Podstawmy powyższe dane do wzoru na średnią harmoniczną:
\(\overline{x}_{H}=\frac{4}{\frac{1}{1}+\frac{1}{2}+\frac{1}{4}+\frac{1}{5}}=\frac{4}{\frac{39}{20}}=4*\frac{20}{39}\approx2,051\)Wychodzi, że średnia gęstość zaludnienia w naszych gminach to trochę ponad 2 tysiące osób na km².
Czy to się zgadza? Jeśli zsumujemy powierzchnie poszczególnych gmin, to otrzymamy 195 km². Pomnóżmy to przez otrzymaną średnią i zobaczmy wynik:
\(195*2,051\approx400\)Super! Udało się wyliczyć, ile osób mieszka przeciętnie na jednym kilometrze kwadratowym w naszych analizowanych gminach.
ważona średnia harmoniczna
No tak, to było dosyć łatwe – a co w sytuacji, kiedy liczba mieszkańców w każdej gminie jest inna? Na przykład druga gmina wcale nie ma 50 km² tylko 200 km²? A kolejne 300 i 400 km²? Czy nadal możemy skorzystać z powyższych obliczeń i stwierdzić, że średnie zaludnienie wynosi 2051 osób/km²?
Sprawdźmy. Ile osób mieszka w naszych gminach w rzeczywistości?
\(1*100+2*200+4*300+5*400=3700\)A jeśli pomnożymy naszą średnią przez zsumowane powierzchnie poszczególnych gmin, to wyjdzie nam:
\(1000*2,051=2051\)Czyli coś się nie zgadza. Niestety, nie możemy skorzystać ze wzoru na zwykłą średnią harmoniczną, trzeba użyć wzoru na ważoną średnią harmoniczną. Wygląda on tak:
\(\overline{x}_{Hw}=\frac{\sum_{i=1}^{n}w_{i}}{\sum_{i=1}^{n}\frac{w_{i}}{x_{i}}}=\frac{w_{1}+w_{2}+\ldots+w_{n}}{\frac{w_{1}}{x_{1}}+\frac{w_{2}}{x_{2}}+\ldots+\frac{w_{n}}{x_{n}}}\)Nasze wagi (kolejne wartości w), to liczba mieszkańców w poszczególnych gminach. Po podstawieniu do wzoru wygląda to następująco:
\(\overline{x}_{Hw}=\frac{100+400+1200+2000}{\frac{100}{1}+\frac{400}{2}+\frac{1200}{4}+\frac{2000}{5}}=\frac{3700}{100+200+300+400}=\frac{3700}{1000}=3,7\)Ważona średnia harmoniczna sprawdziła się idealnie. \(1000*3,7=3700\)
średnia harmoniczna w trapezie
I obiecany deser – średnia harmoniczna w geometrii.
Trapez to taka specyficzna figura geometryczna, która pomaga zaprezentować różne średnie klasyczne w formie graficznej. Dziś opowiem, jak w trapezie można znaleźć średnią harmoniczną.
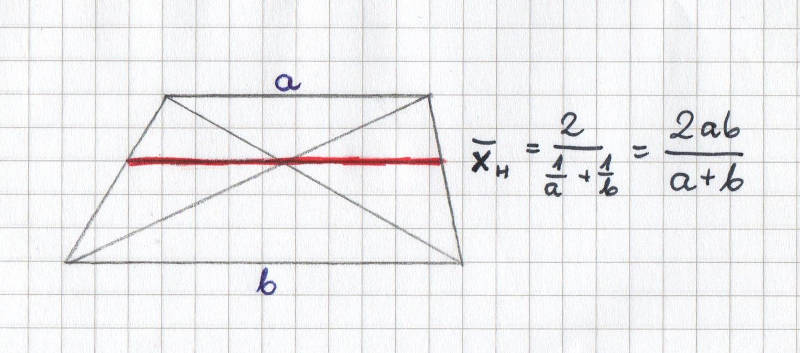
Zaczynamy od narysowania trapezu. Następnie zaznaczamy przekątne i rysujemy linię równoległą do podstaw trapezu, przechodzącą przez miejsce przecięcia obu przekątnych. Linia ta ma długość równą średniej harmonicznej długości obu podstaw, czyli \(\overline{x}_{H}=\frac{2}{\frac{1}{a}+\frac{1}{b}}\) inaczej zapisywane jako \(\overline{x}_{H}=\frac{2ab}{a+b}\)
Nie wierzycie? Narysujcie sobie kilka trapezów, zmierzcie linijką długości podstaw oraz linii przechodzącej przez przecięcie przekątnych. Wyliczcie średnią harmoniczną dla podstaw trapezu. Wychodzi tyle samo?
A może ktoś w komentarzach pokusi się o dowód matematyczny? Zapraszam!
podsumowując…
Mam nadzieję, że powyższe przykłady przybliżyły jeszcze bardziej średnią harmoniczną wszystkim czytelnikom. Z pewnością nie jest to zagadnienie łatwe, ale warto wiedzieć, że sama znajomość średniej arytmetycznej nie rozwiąże wszystkich problemów.
Nie będę przedstawiać średniej harmonicznej dla wynagrodzeń w poszczególnych firmach, które staram się analizować za każdym razem, kiedy przedstawiam kolejne pojęcia. Dlaczego? Bo będzie to tylko obliczona liczba, która nie da nam żadnych informacji o badanej populacji. Średnia harmoniczna powinna być używana w zupełnie innych przypadkach, a średnie wynagrodzenie w firmie lepiej jest obliczyć używając średniej arytmetycznej i tyle.
I jeszcze na koniec mała ciekawostka. Czy wiecie, że średnia harmoniczna jest zawsze mniejsza bądź równa od średniej arytmetycznej?
Droga Czytelniczko! Drogi Czytelniku!
Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.
Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.
A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.
Pozdrawiam Cię serdecznie i życzę miłego dnia!
Krystyna Piątkowska