Obiecałam w ostatnim wpisie o miarach położenia, że opowiem coś również o średniej geometrycznej. Podobnie jak średnia harmoniczna jest ona bardzo zaniedbana, a przydatna w wielu dziedzinach życia. Tak więc dzisiaj „odcinek specjalny” dla fotografów, optyków oraz analityków finansowych. Zapraszam!

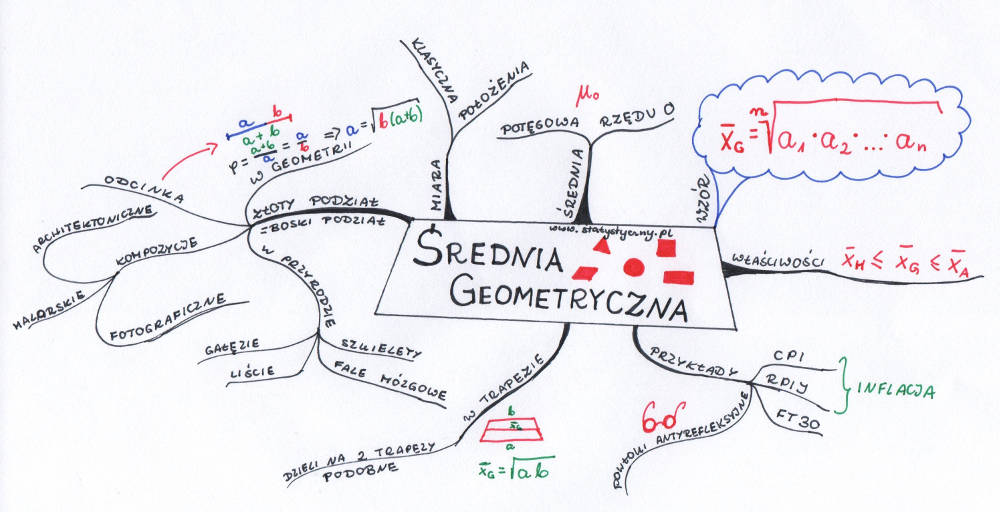
Średnia geometryczna n liczb, to pierwiastek n-tego stopnia z iloczynu tych liczb.

\(\overline{x}_{G}=\sqrt[n]{a_{1}*a_{2}*\ldots*a_{n}}\)

Obliczmy średnią geometryczną dla trzech liczb: 1, 2 oraz 4:

\(\overline{x}_{G}=\sqrt[3]{1*2*4}=\sqrt[3]{8}=2\)

Średnia ta różni się zarówno od średniej arytmetycznej \(\overline{x}_{A}=\frac{1+2+4}{3}=\frac{7}{3}=2\frac{1}{3}\), jak i od średniej harmonicznej \(\overline{x}_{H}=\frac{3}{\frac{1}{1}+\frac{1}{2}+\frac{1}{4}}=\frac{3}{\frac{4}{4}+\frac{2}{4}+\frac{1}{4}}=\frac{3}{\frac{7}{4}}=\frac{12}{7}=1\frac{5}{7}\)

Średnia geometryczna będzie zawsze większa lub równa od średniej harmonicznej oraz mniejsza bądź równa od średniej arytmetycznej.

Przykład indeksów inflacji

Indeksy inflacji liczone są na różne sposoby. Niekiedy używane są średnie arytmetyczne (np. w przypadku RPI – Retail Price Index), a w innych przypadkach średnie geometryczne (RPIJ – Retail Price Index Jevons, CPI – Consumer Price Index). Średnia geometryczna zawsze jest mniejsza od średniej arytmetycznej – stąd liczony w ten sposób współczynnik inflacji również będzie mniejszy.

W Polsce podstawowym podawanym wskaźnikiem inflacji jest wskaźnik cen towarów i usług konsumpcyjnych (odpowiednik CPI). Jest to średnia ważona cen towarów i usług nabywanych przez przeciętne gospodarstwo domowe. Co roku ustala się tzw. statystyczny koszyk zakupów (czyli bada się budżety gospodarstw domowych i ustala, co kupuje takie statystyczne gospodarstwo, uwzględniając udział poszczególnych produktów i usług w łącznych wydatkach). GUS oblicza wskaźnik inflacji na podstawie obserwacji zmian cen usług i towarów ze statystycznego koszyka zakupów.

Również niektóre indeksy giełdowe są liczone za pomocą średniej geometrycznej. Jest to np. angielski indeks FT30.

Przykład – soczewka antyrefleksyjna

Czy ktoś z Czytelników nosi okulary? Ja noszę i pamiętam swoje pierwsze wizyty u optyka, w czasie których słuchałam o różnych powłokach służących do pokrywania soczewek okularowych. Najbardziej polecaną powłoką jest powłoka antyrefleksyjna. I zaraz opowiem, po co używa się takiej powłoki antyrefleksyjnej i dlaczego optycy powinni znać średnią geometryczną.

Szkło i powietrze to są dwa ośrodki o różnych wartościach współczynnika załamania światła. W dużym uproszczeniu wygląda to tak, że światło idzie sobie przez powietrze, dociera do okularów i częściowo przechodzi docierając do oka, a częściowo odbija się od okularów. Powłoka antyrefleksyjna służy do tego, żeby tego światła odbijało się jak najmniej. Pomiędzy dwoma ośrodkami o różnych wartościach współczynnika załamania światła umieszcza się cienką warstwę ośrodka o wartości pośredniej. Dzięki temu współczynnik odbicia światła od tej granicy maleje. Współczynnik obliczamy za pomocą średniej geometrycznej:

\(n_{1}=\sqrt{n_{0}*n_{2}}\)

I taki współczynnik by był najlepszy, ale niestety na razie istnieje tylko w teorii. Najczęściej używane w okularach szkło ma współczynnik załamania światła 1,52. Powietrze ma współczynnik 1. Średnia geometryczna tych dwóch liczb to 1,23. Niestety, nie udało się znaleźć materiału o tak niskim współczynniku, który nadawałby się do pokrywania szkieł okularowych. Najczęściej więc używany jest fluorek magnezu MgF₂ o współczynniku 1,38. Wciąż trwają badania nad materiałami, które jeszcze lepiej pełniłyby funkcję antyrefleksyjną. Być może uczeni znajdą takie substancje, których wartość będzie równa obliczonej średniej geometrycznej.

Zasada złotego podziału

Zasada złotego podziału również jest związana ze średnią geometryczną. Opiera się on na podziale odcinka na dwie części tak, by stosunek długości dłuższej z nich do krótszej był taki sam, jak całego odcinka do części dłuższej. Innymi słowy: długość dłuższej części ma być średnią geometryczną długości krótszej części i całego odcinka.

\(\varphi=\frac{a+b}{a}=\frac{a}{b}\Rightarrow a=\sqrt{b(a+b)}\)

Złoty podział wykorzystuje się bardzo często w kompozycjach architektonicznych, malarskich oraz fotograficznych. Został znaleziony w przyrodzie (m.in. w ułożeniu gałęzi na pniu i w nerwach liści), jest wykorzystywany na rynkach finansowych. W geometrii aż roi się od różnych analiz związanych ze złotym podziałem. Jeśli tylko ktoś jest zainteresowany, to zapraszam do głębszej lektury artykułów na ten temat. A jeśli tylko znajdziecie jakieś ciekawostki – zapraszam do podzielenia się nimi w komentarzach.

średnia geometryczna w trapezie

Podbnie, jak w przypadku średniej harmonicznej, również średnią geometryczną możemy znaleźć w trapezie. Jeżeli liczby a i b potraktujemy jako długości odcinków i zbudujemy trapez o podstawach a i b, to długość odcinka równoległego do podstaw trapezu i dzielącego trapez na dwa trapezy podobne jest równa średniej geometrycznej.

Czy pamiętacie, co to oznacza, że figury są podobne? To takie, które mają ten sam kształt, a różnią się tylko wielkością. Ich boki są odpowiednio do siebie proporcjonalne:

\(\frac{a}{\overline{x}_{G}}=\frac{\overline{x}_{G}}{b}\)

 

\(\overline{x}_{G}^{2}=a*b\)

 

\(\overline{x}_{G}=\sqrt{a*b}\)

 

---

Mam nadzieję, że od dzisiaj średnie arytmetyczna, harmoniczna i geometryczna nie będą dla Was żadnym problemem. Będziecie w stanie rozróżnić, kiedy którą ze średnich należy użyć i czym różnią się między sobą.

Niech żadne zadanie dotyczące miar położenia nie będzie dla Was straszne!

---

Droga Czytelniczko! Drogi Czytelniku!

Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.

Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.

A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.

Pozdrawiam Cię serdecznie i życzę miłego dnia!

Krystyna Piątkowska