„Ratunku, pomocy! Liczę odchylenie standardowe w Excelu (albo innym arkuszu kalkulacyjnym) i wynik mi wychodzi zupełnie inny, niż jak liczyłam na kalkulatorze, na kartce papieru czy po prostu w głowie. Gdzie ten błąd siedzi, bo sprawdzam piąty raz i wciąż mi wychodzi tak samo?”
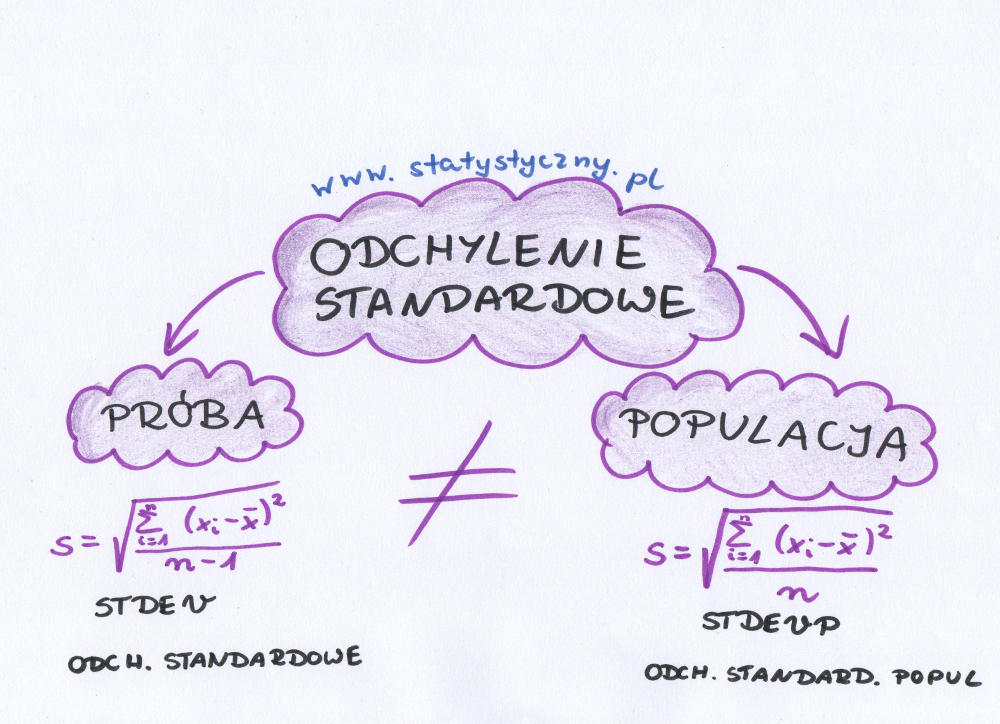
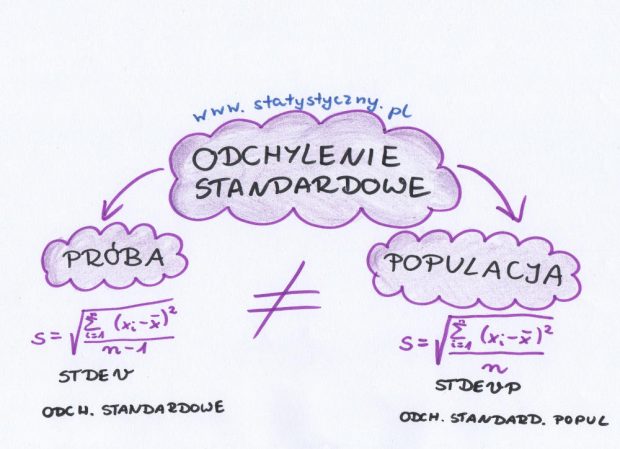
Stali czytelnicy statystycznego już dobrze wiedzą, że wpis o odchyleniu standardowym był dawno temu i potrafią sobie takowe odchylenie wyliczyć. Ale nawet wtedy tylko napomknęłam o czymś takim jak odchylenie standardowe z próby. A licząc właśnie takie odchylenie trzeba uważać, ponieważ wzór jest inny niż na odchylenie standardowe w populacji.
Kilka słów przypomnienia, co to jest odchylenie standardowe
Przypomnijmy na początku, co to jest odchylenie standardowe. Jest to taka miara zmienności rozkładu, która mówi o tym, o ile średnio odchylają się wartości badanej cechy od średniej arytmetycznej. Duże odchylenie standardowe informuje nas o tym, że populacja jest bardzo zróżnicowana, a małe odchylenie standardowe mówi, że poszczególne jednostki skupiają się blisko średniej. Wzorek, przypominam, wygląda tak:
\(s=\sqrt{\frac{\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}}{n}}=\sqrt{\frac{(x_{1}-\overline{x})^{2}+(x_{2}-\overline{x})^{2}+\ldots+(x_{n}-\overline{x})^{2}}{n}}\)Odchylenie standardowe z próby
Tak wyglądało to wszystko w przypadku populacji. A jak będzie wyglądać w przypadku próby? We wzorze mamy do czynienia z jedną, małą, malutką zmianą. A mianowicie w mianowniku ułamka zamiast n pojawia się (n-1).
\(s=\sqrt{\frac{\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}}{n-1}}=\sqrt{\frac{(x_{1}-\overline{x})^{2}+(x_{2}-\overline{x})^{2}+\ldots+(x_{n}-\overline{x})^{2}}{n-1}}\)Co oznacza taka zmiana? W praktyce odchylenie standardowe obliczone z próby (w przypadku takich samych danych) będzie odrobinę większe niż odchylenie dla populacji. Im większa próba, tym bardziej różnica będzie się zacierać. W przypadku małych próbek, zwłaszcza dość mocno zróżnicowanych, zmiana wartości n na (n-1) może znacząco zmienić wynik.
A skąd ta różnica we wzorach? Dlaczego (n-1)? Czy licząc odchylenie standardowe z próby można użyć pierwszego wzoru z samym n? Pamiętajmy, że licząc odchylenie standardowe z próby obliczamy nieznany parametr. Estymujemy wartość odchylenia standardowego dla populacji. W dużym uproszczeniu możemy powiedzieć, że zdajemy sobie sprawę, że nie znamy ani prawdziwej średniej z populacji ani prawdziwego odchylenia standardowego. Spodziewamy się więc, że prawdziwe odchylenie standardowe dla populacji będzie się różnić od tego z próby (chociażby dlatego, że do jego obliczeń używamy estymowanej wartości średniej a nie prawdziwego parametru dla całej populacji). I spodziewając się tej różnicy, akceptujemy większą wartość odchylenia. Ale jeśli nie planujemy estymować, to nie musimy używać wzoru dla próby statystycznej. Kiedy więc możemy użyć wzoru z samym n licząc odchylenie standardowe z próby? Wtedy, kiedy świadomie liczymy wartość odchylenia tylko dla tej próby i nie planujemy uogólniać wyniku na całą populację. Nie traktujemy tego wtedy jako estymatora dla populacji, ale liczymy parametr z próby.
Przykład – kiedy odchylenie standardowe z próby a kiedy z populacji
Teoria teorią. Próby, populacje, n, n-1. Wszystko się miesza i trudno się w tym połapać. Myślę, że najlepiej będzie, kiedy pomoże nam pewien słodki przykład:
- Kupiłam 20 ciastek i chcę wiedzieć, ile średnio ważą i jakie jest odchylenie standardowe wagi moich ciastek. Interesują mnie tylko i wyłącznie moje kupione ciastka. Korzystam więc z pierwszego wzoru na odchylenie standardowe w populacji.
- Kupiłam dokładnie te same 20 ciastek, ale chcę wiedzieć, ile średnio ważą i jakie mają odchylenie standardowe wszystkie ciastka z mojej ulubionej cukierni. Chcę wiedzieć, jaka jest szansa, że następnym razem trafi mi się większe albo mniejsze ciasteczko. Wtedy korzytam z drugiego wzoru na odchylenie standardowe z próby.
- Jestem właścicielem cukierni. Ważę i mierzę wszystkie ciastka. Mogę dokładnie powiedzieć, jaka jest średnia waga upieczonych ciastek. Mogę też wyliczyć odchylenie standardowe dla wszystkich ciastek. Korzystam znów z pierwszego wzoru na odchylenie standardowe w populacji.
Arkusze kalkulacyjne a odchylenie standardowe
I teraz dochodzimy do tego, o czym było na początku. Najczęściej korzystamy w arkuszach kalkulacyjnych z funkcji „stdev” albo „odch.standardowe” zupełnie nieświadomi, że dotyczy ono właśnie odchylenia standardowego z próby. Jeśli chcemy obliczyć odchylenie dla populacji, to musimy użyć funkcji „stdevp” lub „odch.standard.popul” (uwaga! w różnych arkuszach kalkulacyjnych te nazwy mogą się różnić – zdecydowanie proponuję ostrożnie czytać opis funkcji przed użyciem). Pułapką, na którą najczęściej się nabieramy jest ręczne liczenie odchylenia standardowego dla populacji, a w celu sprawdzenia wyniku skorzystanie z funkcji „stdev” w arkuszu. Wtedy właśnie pojawiają się różnice i wielokrotne przeliczenia – gdzie mogliśmy się pomylić? Żeby się nie nabrać – za każdym razem warto przeczytać dokładnie, co oznacza funkcja której zamierzamy użyć.
Podsumowanie
Celowo nie wspominam o tym, że licząc odchylenie standardowe z próby i używając wzoru z samym n byśmy mieli do czynienia z estymatorem obciążonym. Nie wspominam, że (n-1) oznacza nieobciążony estymator wariancji (czy odchylenia standardowego również?). Nie wspominam również o stopniach swobody itp. Być może kiedyś podejmę się wpisu, który będzie objaśniał te zawiłości, ale chwilowo wszystkich bardziej zainteresowanych tematem odsyłam do typowych mądrych podręczników ze statystyki. I nie zdziwcie się, jeśli gdzieś przeczytacie, że to wszystko to było wymyślone dawno temu i tak naprawdę nie ma dużego znaczenia, czy policzycie n czy n-1. Czasem się okazuje, że w statystyce też nie wszystkie pytania mają tylko jedną oczywistą odpowiedź. I statystycy też mogą mieć różne zdanie na temat tego, kiedy jaki wzór należy użyć.
Aby przypomnieć sobie, co już było na statystycznym – zachęcam do korzystania ze spisu treści. Aby być na bieżąco – warto polubić na Facebooku. A najlepiej przekonać do tego jeszcze kilku kolegów – bo dlaczego mają się męczyć wyłącznie z podręcznikową statystyką, skoro można to wszystko przyswoić w wersji przyjemniejszej?
mapa myśli: odchylenie standardowe z próby
Droga Czytelniczko! Drogi Czytelniku!
Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.
Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.
A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.
Pozdrawiam Cię serdecznie i życzę miłego dnia!
Krystyna Piątkowska